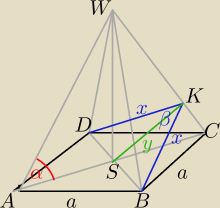
 z tw. cosinusów dla Δ DBC
z tw. cosinusów dla Δ DBC
| a2 | ||
(a√2)2=2x2−2x2cosβ ⇒ cosβ=1− | ||
| x2 |
| √2 | ||
z tw. Pitagorasa dla ΔBSK (y=a | *sinα) | |
| 2 |
| √2 | √2*sinα | |||
x2=(a | )2+(a | )2 | ||
| 2 | 2 |
| a2(1+sin2α) | ||
x2= | ||
| 2 |
| a2 | a2 | 2 | 1+sin2α−2 | |||||||||||
cosβ=1− | =1− | =1− | = | = | ||||||||||
| x2 |
| 1+sin2α | 1+sin2α |
| sin2α−1 | sin2α−sin2−cos2α | −cos2α | ||||
= | = | = | = | |||
| 1+sin2α | cos2α+sin2α+sin2α | cos2α+2sin2α |
| −1 | |||||||||
= | = | |||||||||
| 1+2tg2α |
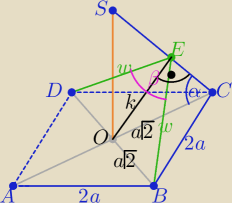 W ΔCOE : k=a√2sinα k2=2a2sin2α
w ΔBOE : w2=k2+2a2 = 2a2(sin2α+1)
Z tw, cosinusów w ΔBED:
W ΔCOE : k=a√2sinα k2=2a2sin2α
w ΔBOE : w2=k2+2a2 = 2a2(sin2α+1)
Z tw, cosinusów w ΔBED:
| 2w2−8a2 | 2 | |||
cosβ= | = 1− | |||
| 2w2 | sin2α+1 |
| sin2α−1 | −cos2α | cos2α | cos2α | |||||
cosβ= | = | =− | |: | |||||
| sin2α+1 | sin2α+1 | cos2α+2sin2α | cos2α |
| 1 | ||
cosβ= − | ||
| 1+2tg2α |