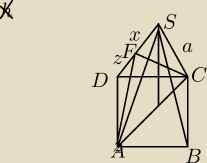Stereometria... trapez: W ostrosłupie prawidłowym czworokątnym kąt nachylenia krawędzi do podstawy jest równy α. Wykaż, wiedząc że β jest kątem między sąsiednimi ścianami bocznymi , że :

	−1
cosβ =
	1+2tg2α

No po prostu nie do zrobienia Siedzę nad tym już godzinę i wychodzi coś niby, ale nie taki wzór końcowy jak powinien... Jakby co, zrobiłem tak: Na początku uznałem krawędź podstawy jako znaną , wyznaczyłem przy jej pomocy krawędź a, trójkąt DFA i FSC , Pitagoras, wyznaczenie "z" wiedząc,że ( a=x+z) , później tw. cosinusów i wychodzi ten cos β − owszem , bez żadnej literki, jedynie funkcje+liczby , lecz nie tak jak w tezie Proszę o pomoc kogoś z jakimiś nowymi pomysłami Chyba, ze źle to pozaznaczałem

trapez: .

trapez: Pomoże ktoś?

trapez: ..

trapez: ...

trapez: ?

trapez: Jeżeli wiecie jak to zrobić , to chociaż napiszcie, to może dalej sobie poradzę

trapez: ..

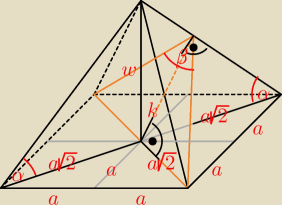Bogdan: U{k}{a√2 = sinα ⇒ k = a√2*sinα

a√2		β		a√2		β
	= tg		⇒		= tg
k		2		a√2*sinα		2

	β		1 − cosβ
Korzystamy z tożsamości: tg		=
	2		√1 − cos2β

1		β		1		(1 − cosβ)2
	= tg		⇒		=		itd.
sinα		2		sin2α		1 − cos2β

trapez: Gościu, jesteś genialny. Nigdy bym na takie coś nie wpadł. Powiedz jeszcze skąd ta tożsamość tgβ/2?

Bogdan:

	α		α		1 − cosα
cos2α = 1 − 2sin2α ⇒ cosα = 1 − 2sin2		⇒ sin2		=
	2		2		2

	α		α		1 + cosα
cos2α = 2cos2α − 1 ⇒ cosα = 2cos2		− 1 ⇒ cos2		=
	2		2		2

	α		1 − cosα		1 − cosα		1 − cosα
tg2		=		=		*		=
	2		1 + cosα		1 + cosα		1 − cosα

	(1 − cosα)2		α
=		⇒ tg		= ...
	1 − cos2α		2