planimetria domino: W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość a , druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu. Zastanawia mnie fakt, skąd wiemy, że odcinek ten jest równoległy do podstaw oraz dlaczego jest on długości średniej arytmetycznej dwóch podstaw. Ewentualnie jak działa tutaj twierdzenie Talesa i podobieństwo tak jak wykonano te zadanie tutaj: https://zadania.info/d1409/1502808

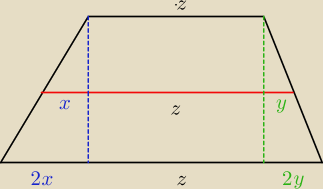
wredulus_pospolitus: z podobieństwa trójkątów wyznaczasz proporcje wskazane na rysunku chociaż Ty akurat masz w zadaniu trapez prostokątny − co nie ma znaczenia

	podstawa1 + podstawa2
I mamy: z + (2x + z + 2y = 2*(x+z+y) −−−>		= dlugość
	2

odcinka łączącego środki ramion

domino: dobra, a skąd wiemy, że ten odcinek jest równoległy do podstaw?

chichi: https://matematykaszkolna.pl/forum/19803.html Tutaj znajduje się kilka dowodów pokazujących, że odcinek łączący środki ramion trapezu jest równoległy do podstaw. Rzuć okiem

domino: Tego szukałem, dzięki!

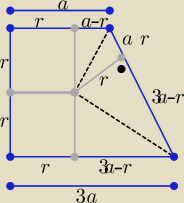
Eta: Inny sposób obliczenia pola ( niż podali w info)

	3a+a
P=		*2r = 4ar
	2

r²=(a−r)(3a−r) ⇒ 3a²=4ar P=3a² =======