udowodnienie Paula :): Wykaż, że odcinek łączący środki ramion trapezu jest równoległy do jego podstaw, a jego długośc jest średnią arytmetyczną długości podstaw trapezu. Proszę o pomoc w tym zadaniu, najlepiej z rysunkiem, gdyż sama nie potrafię tego za bardzo zrobic ..

Paulaaa: to trzeba zrobic za pomocą wektorów ..

tim: Wektorami?

Paula :): wie ktos jak to zrobic?

Eta: Najprościej tak jak podpowiada Tim za chwilę podam inny sposób

Paula :): a jak to wektorem zrobic?

Paula :): pomoze ktos

Eta: Pomogę za godz. , bo muszę teraz wyjść

Paula :): droga Eto, czy wróciłaś już ? : >

Eta: Tak jestem , pomagam , rysuję więc troszkę potrwa, cierpliwości

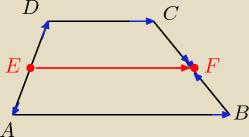
Eta: Załozenie: → → AB I I DC i IAEI=IEDI i IBFI = IFCI Teza:

	IABI + IDCI
IEFI =
	2

i EF I I AB I I DC Dowód: korzystając z sumy wektorów mamy : → → → → EF = ED + DC + CF i → → → → EF = EA + AB + BF dodając stronami otrzymamy: −−−−−−−−−−−−−−−−−−−− 2*EF = ED + EA +DC + AB + CF + BF ( pisz wszędzie strzałki ( bo mi nie wygodnie ponieważ : wektory ED i EA oraz BF i CF są przeciwne więc ED = − EA i BF = − CF ( pisz strazałki to otrzymasz 2EF = ED − ED +DC + AB + CF − CF= AD + DC

	IABI + IDCI
więc I EFI=		−−− to średnia arytm długości podstaw
	2

teraz z załozenia mamy ,że : AB I I DC , więc wektor sumy jest też równoległy do EF zatem EF I I AB I I DC c.n. o. PS: pamiętaj o pisaniu strzałek nad wektorami

Eta: To jeden ze sposobów ( jest jeszcze inny .... podawać ?

Paula :): ee.. myślę, że to wystarczy. potrzebuję teraz trochę czasu na analizę. ewentualne pytania zadam za chwilkę ; ) dziękuję bardzo!

Eta: ok

Bogdan:

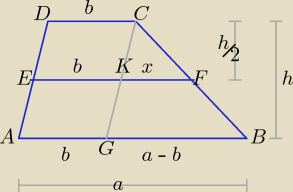
	a − b		h		a − b
Z podobieństwa trójkątów: GBC i KFC:		=		⇒ x =
	x		1   h 2		2

	a − b		2b + a − b		a + b
|EF| = b + x = b +		=		=
	2		2		2

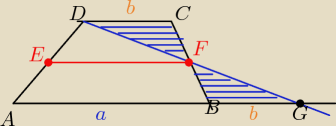
Eta: Można też tak ΔBFG przystaje do ΔDFC z cechy ( k,b,k) bo kąty ma ją równe miary i IBFI = IFCI EF łaczy środki boków ΔAGD

	a +b
więc IEFI = 12*IAGI=
	2

oraz EF I I AB c.b.d.o.

Bogdan:

Eta: He,he.... pierwszy raz taki ładny rysunek mi wyszedł,

AROB: Gratuluję,Eta, jest śliczny! Dobranoc na dziś. Odpocznij wreszcie.

kapitan47: dlaczego z : "EF łaczy środki boków ΔAGD a +b więc IEFI = 12*IAGI= 2 oraz EF I I AB " wynika równoległość

Eta: ΔAGD ~ ΔEFD w skali k=2

	1		a+b
to |EF|=		|AG| =
	2		2

osas: tez tak mysle