Wykaż, że pole równoległoboku jest nie większe niż połowa pola trójkąta ABC. Jasiek: W trójkącie ostrokątnym ABC na jednym z boków obrano punkt D. Przez punkt D poprowadzono proste równoległe do dwóch pozostałych boków trójkąta, dzieląc trójkąt ABC na dwa mniejsze trójkąty i równoległobok. Wykaż, że pole równoległoboku jest nie większe niż połowa pola trójkąta ABC. https://matematykaszkolna.pl/forum/398030.html Próbowałem zrobić to zadanie według rad z tego posta, ale nie rozumiem ich do końca

Blee: A czego dokładnie nie rozumiesz?

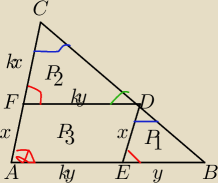
Jasiek: Czy moje rozwiązanie jest poprawne? T: P3 ≤ (P1+P2+P3)/2 → P3 ≤ P1 + P2 ΔDEB ∼ ΔCFD (kkk) w skali k, k > 0 P1 = xy/2 * sinα P2 = k²*xy/2 * sinα P3 = kxy * sinα Dowód niewprost: kxy * sinα > xy/2 * sinα + k²*xy/2 * sinα |:sinα kxy > xy/2 + k²*xy/2 |*2 2kxy > xy + k²*xy |:xy k² − 2k + 1 < 0 (k − 1)² < 0 sprzeczność c. n. u.

wredulus_pospolitus: jest ok chociaż ja osobiście raczej bym pokazywał, że

	1		1
P3 = kxysinα ≤		(k+1)2xysinα =		PABC
	4		2

ale to na jedno wychodzi