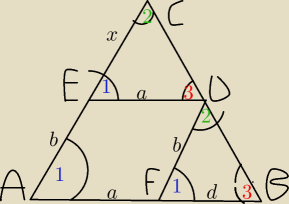
dowód planimetria Frajvald: Mógłby ktoś pomóc dokończyć takie zadanie? W trójkącie ostrokątnym ABC na jednym z boków obrano punkt D . Przez punkt D poprowadzono proste równoległe do dwóch pozostałych boków trójkąta, dzieląc trójkąt ABC na dwa mniejsze trójkąty i równoległobok. Wykaż, że pole równoległoboku jest nie większe niż połowa pola trójkąta ABC.

	1
kąt 1 to kąt alpha. Obliczyłem pole trójkąta FDB=		*b*d*sin a
	2

	1		a2*b
pole trójkąta EDC =		*
	2		d

	1
pole równoległoboku AFDE =		*b*a*sin a
	2

i nie wiem jak skończyć, mógłby ktoś coś? poradzić

wredulus_pospolitus: Z Tw. Talesa wiemy, że:

x		x+b
	=
a		a+d

	b		x+b
Ale także:		=
	d		a+d

z tego wiemy, że:

PCDE		a2
	= (		)2
PABC		a+d

PDBF		d2
	= (		)2
PABC		a+d

PCDE + PDBF		a2+d2
	=
PABC		(a+d)2

	PAFDE		2ad
Z tego wynika, że		=
	PABC		(a+d)2

oznaczmy: d = a*k ; gdzie k ∊ R₊ ... istotne: a+d = const. wtedy:

2ad		2a2k		2k
	=		=		= f(k)
(a+d)2		(a(k+1))2		(k +1)2

szukasz maksimum funkcji f(k) czyli pochodna i jedziesz 'z koksem' wartość funkcji w maksimum da Ci maksymalny stosunek pola równoległoboka do pola dużego trójkąta

wredulus_pospolitus: oczywiście można też zrobić a+d = const. −> a = const. − d Istotne by const. w momencie liczenia pochodnej to była STAŁA.

jc: Pole dwóch trójkątów jest proporcjonalne do CD²+BD², a suma ta jest najmniejsz, gdy CD=BD. Wtedy oba trójkąty mają pole równe połowie pola dużego trójkąta.

	1		1		1
(CD2+BD2)=		[ (CD+BD)2 + (CD−BD)2] =		(CD+BD)2=		BD2.
	2		2		2

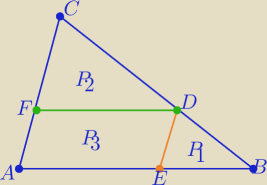
Eta: Wykaż,że zachodzą zależności : P(ABC)=P=(√P₁+√P₂)² i P₃=2√P₁*P₂ A teraz tezę już łatwo wykazać

jc: Mała pomyłka. Zamiast drugiego znaku = powinien być znak ≥.

Frajvald: Bardzo dziękuje wszystkim za odpowiedzi

silnia: z tego wiemy, że: PCDE a2 = ( )2 PABC a+d PDBF d2 = ( )2 PABC a+d Dlaczego? @wredulus pospolitus