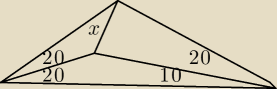
kąty anek: Korystając z danych na rysunku wyznacz miarę kąta x. Te kąty są w stopniach. Nic nie wiadomo o bokach, ani o tych odcinkach wenątrz, tylko to co na rysunku.

ICSP: https://matematykaszkolna.pl/forum/402511.html

anek: ICSP , a jakie ostało ono rozwiązne tutaj: https://images90.fotosik.pl/385/931ae62231a395ce.jpg

ICSP: Zaczekaj na Etę Ja takich zwyrodniałych rzeczy nie czytam.

antek: Czemu zwyrodniałe?

a7:

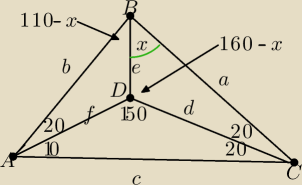
a		c
	=		⇒c=2acos20
sin30		cos20

c		f		c		f
	=		⇒		=		⇒ ...⇒ f=2asin40
sin150		sin20		cos60		sin20

f		e
	=
sin(110−x)		sin20

a		e
	=
sin(160−x)		sin20

	2asin40
U{a}{sin(160−x)=
	sin(110−x)

sin(110−x)=2sin40cos(70−x) dla x=30 sin80=2sin40cos40 sin80=sin80 prawda x=30 ====

antek: A o co chodzi w tym co ja podałem bo mam tylko rysunek? i chce tez tamto zrozumiec

a7: ja narysowałam to samo tylko w lustrzanym odbiciu, bo tak mi łatwiej było myśleć

a7:

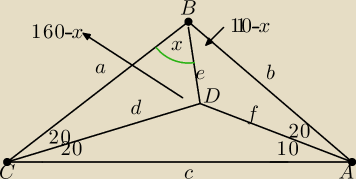
a7: chodzi o to , że korzystamy z twierdzenia sinusów i zauważamy, że można dojść do ładnego równania trygonometrycznego, które jest spełnione dla x=30

antek: Chodiło mi o to co ja podałem w linku. A jak rozwiazć to równanie sin(110−x)=2sin40cos(70−x)

a7: zauważamy, że dla 30^o jest spełnione

a7: nie rozumiem, w którym linku, przecież to to chyba co z godziny 08:17, czyli to które rozwiązałam

a7: 14:17 korzystamy z wzoru że sin(2α)=2sinαcosα

Iryt: sin(110−x)=2sin40*cos(70−x), x − kąt ostry sin(110−x)=sin(40+70−x)+sin(40−70+x) z wzoru sin(x+y)+sin(x−y)=2 sinx*cosy sin(110−x)=sin(110−x)+sin (x−30)⇔ sin(x−30^o)=0 x−30^o= 0^o +kπ x=30⁰+kπ, k=0 x=30^o

antek: nie ten z 11.18

Mila: 17:15 masz odpowiedź na Twoje pytanie z 14:15. 11:18 nie analizowałam , nawet nie zauważyłam linka. Zobaczę co tam jest, skąd ten link?

antek: nie wiem czy dobrze, nalezione w necie

xx: Bez trygonometrii ?

Mila: Da się. Tylko z dobrym rysunkiem jest kłopot w tym edytorze. Napiszę.

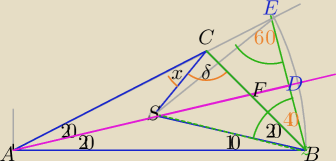
Mila: 1) x+δ=110^o 2) AF− dwusieczna kąta A 3) Przedłużam AC tak, aby: |AE|=|AB| ΔABE −Δrównoramienny, |BC|=|BE| ∡E≡∡B=70^o, |∡CBE|=40^o ΔSBE− Δrównoboczny AD− symetralna BE⇒|SB|=|SE|=|EB| ⇒ ΔSCB− Δrównoramienny o kącie 20^o między ramionami δ=(180−20):2=80 4) x+80^o=110^o x=30^o ======

Mila: Proszę ite o ładny rysunek w geogebrze

ite: przeniesione do geogebry : ) https://www.geogebra.org/geometry/m2ddxphm

Mila: Dziękuję. Rysunek piękny .