kąty

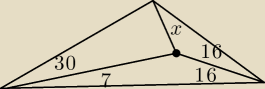
kąty g123: rysunek

Dany jest trójkąt , w którym wybrano dowlny punkt. Kąty na rysunku są podane w stopniach. Oblicz miarę kąta oznaczonego x.

3 cze 08:22

getin: nie wyliczysz tego, za mało danych można tylko wywnioskować że miara kąta x nie przekroczy 111^o

3 cze 10:26

g123: A nie bedzie to 14 stopni?

3 cze 10:51

Bleee: Jakie 14 stopni?

3 cze 10:55

g123: 14^o

3 cze 12:28

getin: równie dobrze ja mogę napisać że x = 20^o po prostu brakuje danych dotyczących długości odcinków i bez tych danych nie wyliczysz jednoznacznie tego iksa

3 cze 13:43

g123: Może ktoś to inny sprawdzić bo getin na pewo sie myli

3 cze 22:07

Eta: x= 7^o

3 cze 22:26

g123: Co 7^o

3 cze 22:28

Eta:

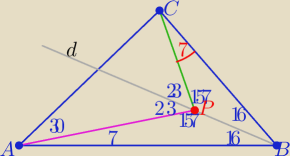
d −− dwusieczna kąta ABC

3 cze 22:36

Eta: Z rysunku wynika ,że punkt K −− wybrano na dwusiecznej kąta ABC ( na rysunku zamiast P ma być K

3 cze 22:39

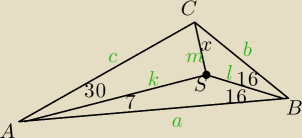
getin: rysunek

da się to wyliczyć, zwracam honor zmyliło mnie to "dowolny punkt" w treści zadania ten punkt jednak nie jest dowolny bo są podane kąty Rozwiązanie: |∡ABS| = 180^o−7^o−16^o = 157^o |∡ACB| = 180^o−37^o−32^o = 111^o z tw. sinusów w ΔABS

a		k		a*sin16^o
	=		→ k =
sin157^o		sin16^o		sin157^o

a		l		a*sin7^o
	=		→ l =
sin157^o		sin7^o		sin157^o

z tw. sinusów w ΔABC

a		b		a*sin37^o
	=		→ b =
sin111^o		sin37^o		sin111^o

a		c		a*sin32^o
	=		→ c =
sin111^o		sin32^o		sin111^o

z tw. cosinusów w ΔSBC m² = l² + b² − 2*l*b*cos16^o

	a*sin7^o		a*sin37^o
podstawiając wcześniejsze l =		oraz b =
	sin157^o		sin111^o

otrzymujemy m = a*√sin7^o/sin²157^o + sin²37^o/sin²111^o − 2sin7^o*sin37^o*cos16^o/(sin157^o*sin111^o) z tw. sinusów w ΔSBC

l		m
	=
sinx		sin16^o

czyli

	l*sin16^o
sinx =
	m

wstawiając do tego wyliczone wcześniej l oraz m uzależnione od a otrzymujemy sinx = (sin16^o*sin7^o) / (sin157^o * √sin7^o/sin²157^o + sin²37^o/sin²111^o − 2sin7^o*sin37^o*cos16^o/(sin157^o*sin111^o)) czyli sinx jest ułamkiem o liczniku sin16^o*sin7^o i mianowniku sin157^o * √sin7^o/sin²157^o + sin²37^o/sin²111^o − 2sin7^o*sin37^o*cos16^o/(sin157^o*sin111^o) z tego wychodzi sinx ≈ 0,1163 oto dowód: https://www.wolframalpha.com/input/?i=%28sin16deg*sin7deg%29%2F%28sqrt%28sin%5E2%287deg%29%2Fsin%5E2%28157deg%29+%2B+sin%5E2%2837deg%29%2Fsin%5E2%28111deg%29+-+%282*sin%287deg%29*sin%2837deg%29*cos%2816deg%29%29%2F%28sin%28157deg%29*sin%28111deg%29%29%29%29 czyli x ≈ 6,68^o czyli w jeszcze większym przybliżeniu wyjdzie wspomniane wyżej siedem stopni

3 cze 22:57

g123: Nie rozumiem rozwiązania Ety skąd te 23^o i skąd BPC=157^o

3 cze 23:35

wredulus_pospolitus: 1) 180 − ( 7 + 16) = 157 (dolny kąt) 180 − 157 = 23 (dolny kąt) 2) Odcinek BK leży na DWUSIECZNEJ kąt przy wierzchołku B. Tak więc cała ta dwusieczna będzie też dwusieczną dla kątów przy K ... stąd mamy górne kąty 23 i 157 3) związku z tym kąt x = 7 (trójkąty podobne, cecha KKK .... lub jak wolisz − suma kątów w trójkącie równa 180)

3 cze 23:38

Eta:

3 cze 23:39

g123: https://pl.wikipedia.org/wiki/Twierdzenie_Cevy_(trygonometryczne) A z tego powyższego twierdzenia: sin30/sin7 * sin16/sin16 *sinx/sin(111−x)=1

3 cze 23:42

Eta: Ale się oliczyłeś

getin Użyłeś F−16 do unicestwienia małej muszki emotka

3 cze 23:43

g123: A czy dobrze jest z tego Tw Cevy?

3 cze 23:48

Eta: Następny wyciąga armatę

3 cze 23:48

g123: https://www.wolframalpha.com/input/?i=sin30%2Fsin7+*+sin16%2Fsin16+*sin7%2Fsin%28111%E2%88%927%29%3D1 A czemu tu jest źle?

3 cze 23:59

g123:

4 cze 00:29

g123: up

4 cze 11:05

a7: ja też nie rozumiem

4 cze 12:25

a7: Czy ktoś rozumie dlaczego jest 7 i 157 stopni w trójkącie BPC (u Ety) vel BKC (u Ety) vel BSC (u getina)

4 cze 12:29

g123: moze ktos jeszcze zerknie

4 cze 13:36

getin: a jednak odpowiedź podana przez g123 okazała się poprawna, ja gdzieś się musiałem pomylić przy wpisywaniu do wolframa Z układu równań

	a*sin37^o
b =
	sin111^o

	a*sin7^o
l =
	sin157^o

m² = l² + b² − 2*l*b*cos16^o

	l*sin16^o
sinx =
	m

przyjmując sin7^o ≈ 0,12187 sin16^o ≈ 0,27564 sin157^o ≈ 0,39073 sin37^o ≈ 0,60182 sin111^o ≈ 0,93358 cos16^o ≈ 0,96126 wychodzi b ≈ 0,64464a l ≈ 0,3119a m² ≈ 0,09728a² + 0,41556a² − 2*0,3119a*0,64464a*0,96126 m² ≈ 0,126292a² m ≈ 0,355376a

	0,3119a*0,27564
sinx ≈
	0,355376a

sinx ≈ 0,2419 x ≈ 13,99871^o ≈ 14^o Narysowałem sobie ten trójkąt na kartce, zachowując podane w zadaniu kąty i zmierzyłem kąt x. Wyszedł 14 stopni

4 cze 14:00

ABC: dla 14 stopni twoja tożsamość jest prawdziwa https://www.wolframalpha.com/input/?i=sin30%2Fsin7+*+sin16%2Fsin16+*sin14%2Fsin%28111%E2%88%9214%29%3D1

4 cze 14:00

ABC: cytując wredulusa gdzieś tam wyżej : "Odcinek BK leży na DWUSIECZNEJ kąt przy wierzchołku B. Tak więc cała ta dwusieczna będzie też dwusieczną dla kątów przy K ... stąd mamy górne kąty 23 i 157" nie podał dowodu tej nieoczywistej własności, która na moje oko nie zachodzi emotka

4 cze 14:09

a7: no właśnie odcinki b i a musiałyby być chyba równe, a nie są

4 cze 14:15

23: Też Uważam, że Tam będzie 14 stopni i wcale przy K nie Będzie dwusiecznej.

4 cze 14:39

23: w sensie d nie bedzie dwusieczna kata APC na rysunku Ety

4 cze 14:42

a7:

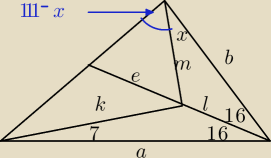
l		m		l		k		k*sin7
	=		oraz		=		czyli l=		czyli
sinx		sin16		sin7		sin16		sin16

	k
sinx=		sin7
	m

dalej sinx=2sin(111−x)*sin7 czy teraz nie jest już łatwo? sinx=2sin7cos(21−x) sinx=2sin7cos7 (? 21−x=7 x=14) sinx=sin14 x=14 trochę w tej końcówce chyba trzeba coś jeszcze doszlifować, ale to chyba dość szybki i skuteczny sposób

4 cze 18:20

a7:

	k		m
a przepraszam jeszcze nie przepisałam z kartki tutaj		=		czyli
	sin(11−x)		sin30

	k
m=
	2sin(111−x)

4 cze 18:23

a7: sin(111−x)

4 cze 18:23

Eta: Sorry za zamieszanie emotka

To nie była "muszka" − tylko "bombowiec"

Cała sytuacja spowodowała,że na pomoc "F−16" ruszyły wszystkie siły ( getin, a7 , ABC

) Jedynie wredulus uwierzył kobiEcie

Pozdrawiam cieplutko Wszystkich emotka

4 cze 18:33

wredulus_pospolitus: Bo ja wszystko co piszesz przyjmuję jako prawdę objawioną emotka

Nie śmiem się nie zgodzić z kobiEtą emotka

4 cze 18:34

Eta: A przecież wiadomo,że "kobiEta" zmienną jest

4 cze 18:36

anek: Hej podobne zdanie tutaj, ktoś zerknie i wyjaśni ten sposób: https://matematykaszkolna.pl/forum/403154.html

21 cze 11:19