Ekstrema i monotoniczność funkcji
Agaa: Znajdź ekstrema lokalne funkcji i zbadaj jej monotoniczność:
a) f(x)=1−
x2+x+1x2−1 x
2+x+1 przez x
2−1
b) f(x)=
exx+2 (e
x przez x+2) − tak piszę bo na równaniu średnio widać
Bardzo proszę o pomoc

17 cze 09:53
Qulka: trzeba używać dużego U do ułamków

w a sprowadź do wspólnego mianownika, będzie trochę ładniejszy licznik

17 cze 09:56
janek191:
Pisz ułamki korzystając z litery U.
17 cze 09:56
17 cze 09:57
17 cze 10:05
janek191:
| | ex | |
b) f(x) = |
| x ≠ − 2 |
| | x + 2 | |
| | ex *(x +2) − ex | | x*ex + ex | | ex*(x + 1) | |
f '(x) = |
| = |
| = |
| |
| | (x + 2)2 | | (x +2)2 | | (x +2)2 | |
f '(x) = 0 ⇔ x = − 1
Dla x < −1 jest f'(x) < 0
Dla x > − 1 jest f '(x) >0
f ma w punkcie x = − 1 minimum lokalne.
x = −2 asymptota pionowa
lim f(x) = −
∞
x→ −2
−
lim f(x) = +
∞
x→ − 2
+
zatem
f maleje w ( −
∞, − 2)
f maleje w ( −2, − 1)
f rośnie w ( − 1 , +
∞)
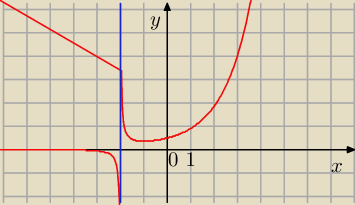
Patrz też na wykres funkcji f.
17 cze 10:07
janek191:

| | ex | |
b) f(x) = |
| x ≠ − 2 |
| | x + 2 | |
| | ex *(x +2) − ex | | x*ex + ex | | ex*(x + 1) | |
f '(x) = |
| = |
| = |
| |
| | (x + 2)2 | | (x +2)2 | | (x +2)2 | |
f '(x) = 0 ⇔ x = − 1
Dla x < −1 jest f'(x) < 0
Dla x > − 1 jest f '(x) >0
f ma w punkcie x = − 1 minimum lokalne.
x = −2 asymptota pionowa
lim f(x) = −
∞
x→ −2
−
lim f(x) = +
∞
x→ − 2
+
zatem
f maleje w ( −
∞, − 2)
f maleje w ( −2, − 1)
f rośnie w ( − 1 , +
∞)
Patrz też na wykres funkcji f.
17 cze 10:07
janek191:
Połamało mi wykres

17 cze 10:09
Qulka: zawsze tak robi jak ma nieskończoności

17 cze 10:10
ABC:
Eta jest cwana i umie rysować żeby nie łamało, to kwestia dobrania skali

17 cze 10:18
janek191:
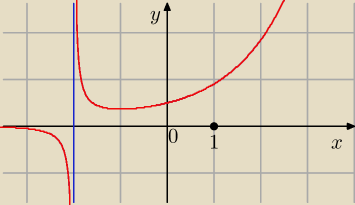
17 cze 10:35
17 cze 10:49

 w a sprowadź do wspólnego mianownika, będzie trochę ładniejszy licznik
w a sprowadź do wspólnego mianownika, będzie trochę ładniejszy licznik 






 super
super 
