zadanie optymilizacyjne anonim123: https://matematyka.pl/viewtopic.php?t=377444 Nie rozumiem rozwiązania Kerajsa Nie wiem o co chodzi w tym momencie i dalej też nie wiem Dla jakiego punktu styczna do paraboli jest równoległa do odcinka AB ?

anonim123: Skąd tam się wzięła informacja o paraboli?

ygrek: https://matematykaszkolna.pl/forum/281315.html

anonim123: A jak to zrobić sposobem Kerjasa?

anonim123: ?

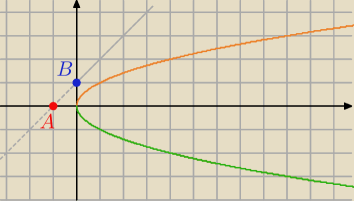
xyz: ta "parabola" to dwa wykresy 1) y = √x (pomaranczowy) 2) y = −√x (zielony) On szuka stycznej do tej "paraboli" i rownoleglej do prostej AB wiadomo, ze punkt C(x_c, √x_c) Aczkolwiek wydaje mi sie ze szuka stycznej do gornej polowy "paraboli" czyli funkcji y=√x, bo tylko te czesc jest sens rozpatrywac. Czyli mamy funkcje y = √x, zapiszmy to jako f(x) = √x (Wiadomo, ze pochodna w punkcie to wspolczynnik kierunkowy prostej stycznej) zatem pochodna:

	1
f'(x) = (√x)' =
	2√x

prosta AB ma wspolczynnik kierunkowy:

	YB−YA		1−0		1
a =		=		=		= 1
	XB−XA		0−(−1)		1

teraz ta pochodna w punkcie ma wynosic tyle ile wspolczynnik prostej AB czyli 1

	1
f'(xc) =		= 1
	2√xc

stad 2√x_c = 1 √x_c = 2 x_c = 4 Czy to rozw. jest prostsze, no nie powiedzialbym...

anonim123: Dzięki