Rachunek różniczkowy, raczej proste zadania
Michał: Witam,
Mam problem z zadaniami z Aksjomatu. Dotyczą one rachunku różniczkowego.
Pierwsze to:
1.Na paraboli y=3x
2−5x+6 znajdź punkt leżący najbliżej punktu (3,2).
Tutaj teoretycznie wiem jak to zrobić, bo myślę że muszę wyznaczyć pochodną, następnie napisać
równanie prostej stycznej do paraboli, a potem prostą prostopadłą do punktu (3,2) i zobaczyć w
jakim miejscu przecina, tylko sporo gorzej z realizacją

2.W trójkącie ABC wierzchołek C leży na wykresie funkcji f(x)=
√x oraz A=(−1,0) i B(0,1).
Wyznacz współrzędne punktu C tak, aby pole trójkąta ABC było jak najmniejsze.
Tutaj chciałem oprzeć się na wzorze Herona, ale nie wygląda to jakkolwiek zachęcająco. Może
jest jakaś inna droga? Teoretycznie to wiem jaki to będzie punkt, bo to będzie ten leżący na
prostej AB(czyli taki gdy trójkąt nie istnieje−tak mi sie wydaje), ale na pochodne to nie wiem
jak zrobić.
Bardzo bym prosił o zrobienie, lub pomoc w zrobieniu tych zadań. W nagrodę mogę wysłać

albo

ale także


23 lut 20:07
Michał: Edit. w 2 wykres
√x dotyczy tylko liczb dodatnich, teraz to zauważyłem.

23 lut 20:20
===:
1)
... JUŻ W OPISIE PROBLEM
nie znam prostej prostopadłej do punktu i też tego nie zrealizowałbym −

23 lut 20:24
Kacper:
Zadanie 2 → wzór z wyznacznika będzie ok.
Zadanie 1
P=(x,3x2−5x+6) − punkt na paraboli
A=(3,2)
|AP|=√(3−x)2+(3x2−5x+6−2)2=√x2−6x+9+9 x4−30 x3+49 x2−40 x+16
=√9 x4−30 x3+50 x2−46 x+25
Teraz chcemy, żeby odcinek |AP| był najkrótszy, czyli możemy szukać minimum kwadratu tej
odległości. Wobec tego szukamy minimum funkcji f(x)=9 x4−30 x3+50 x2−46 x+25.
To minimum mamy dla x=1, zatem nasz punkt ma współrzędne P(1,4).
23 lut 20:26
Michał: A mógłbyś napisać jaki Tobie ten wzór z wyznacznika wychodzi? Może robię gdzieś błąd. Dzięki

23 lut 20:35
Mila:
AB:
k: y=x+1⇔x−y+1=0
C=(x,
√x), x≥0
| | |x−√x+1| | |
d(C,k))= |
| odległość punktu C od prostej AB: y=x+1 |
| | √12+12 | |
| | √2 | | |x−√x+1| | | |x−√x+1| | |
PΔ= |
| * |
| = |
| |
| | 2 | | √2 | | 2 | |
| | 1 | |
P(x)= |
| *(x−√x+1) dla x≥0 |
| | 2 | |
| | 1 | | 1 | |
P'(x)= |
| *(1− |
| ) , x>0 |
| | 2 | | 2√x | |
23 lut 20:44
Kacper:
Masz rozwiązanie klasyczne od
Mili 

Ja dziś czasu nie mam.
23 lut 20:46
Mila:
23 lut 20:47
23 lut 20:51
prosta: W pierwszym zadaniu długość odcinka AP , gdzie P jest punktem paraboli....otrzymamy funkcję z
niewiadomą x, potem pochodna itd
23 lut 21:07
prosta: już zrobione wyżej, przegapiłam

23 lut 21:08
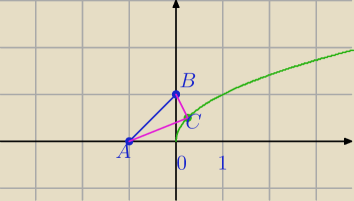
 2.W trójkącie ABC wierzchołek C leży na wykresie funkcji f(x)=√x oraz A=(−1,0) i B(0,1).
Wyznacz współrzędne punktu C tak, aby pole trójkąta ABC było jak najmniejsze.
Tutaj chciałem oprzeć się na wzorze Herona, ale nie wygląda to jakkolwiek zachęcająco. Może
jest jakaś inna droga? Teoretycznie to wiem jaki to będzie punkt, bo to będzie ten leżący na
prostej AB(czyli taki gdy trójkąt nie istnieje−tak mi sie wydaje), ale na pochodne to nie wiem
jak zrobić.
Bardzo bym prosił o zrobienie, lub pomoc w zrobieniu tych zadań. W nagrodę mogę wysłać
2.W trójkącie ABC wierzchołek C leży na wykresie funkcji f(x)=√x oraz A=(−1,0) i B(0,1).
Wyznacz współrzędne punktu C tak, aby pole trójkąta ABC było jak najmniejsze.
Tutaj chciałem oprzeć się na wzorze Herona, ale nie wygląda to jakkolwiek zachęcająco. Może
jest jakaś inna droga? Teoretycznie to wiem jaki to będzie punkt, bo to będzie ten leżący na
prostej AB(czyli taki gdy trójkąt nie istnieje−tak mi sie wydaje), ale na pochodne to nie wiem
jak zrobić.
Bardzo bym prosił o zrobienie, lub pomoc w zrobieniu tych zadań. W nagrodę mogę wysłać  albo
albo  ale także
ale także 




 AB:
k: y=x+1⇔x−y+1=0
C=(x, √x), x≥0
AB:
k: y=x+1⇔x−y+1=0
C=(x, √x), x≥0

 Ja dziś czasu nie mam.
Ja dziś czasu nie mam.









