Wyznaczyć końce odcinka.
Kacper: Jest prosta y=−(4/5)x oraz y=(1/3)x. Punkt D (−1 ; 2,5) jest środkiem odcinka, którego końce
(B, C) leżą na tych prostych. Trzeba wyznaczyć te końce. Wyznaczyłem wzór prostej
przechodzącej przez D y=(b−2,5)x+b. Zgadując mogę wyznaczyć te końce B(−5, 1) oraz C(3,1) bo
tylko one spełniają równania −2=xB+xC oraz 5=yB+yC. Jak zrobić to bardziej matematycznie? Z
góry dziękuję za pomoc.
10 cze 09:12
10 cze 09:58
Kacper: dzięki
10 cze 10:00
Kacper: Zupełnie nie pomyślałem o zwyczajnym podstawieniu pod y−ki x−ów
10 cze 10:10
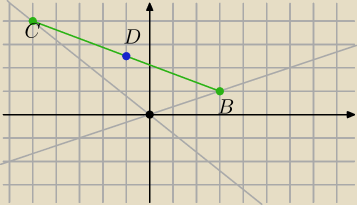 B=(x__B, 1/3xB) C=(xC,−4/5xC)
punkt D jest srodkiem odcinka CB więc jego współrzedne spełniają układ równań
https://matematykaszkolna.pl/strona/1750.html
B=(x__B, 1/3xB) C=(xC,−4/5xC)
punkt D jest srodkiem odcinka CB więc jego współrzedne spełniają układ równań
https://matematykaszkolna.pl/strona/1750.html