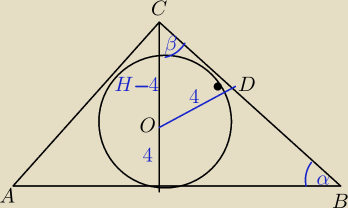
optymalizacja salamandra: Na kuli o promieniu R=4 cm opisujemy stożki o promieniu r i wysokości H. Spośród wszystkich takich stożków wyznacz ten, który ma największą objętość. Czy można tutaj jakoś z podobieństwa to ruszyć?

a7: https://matematykaszkolna.pl/strona/835.html

salamandra: Wiem, moje pytanie było, czy z podobieństwa można, tak jak zaznaczyłem.

a7: rozumiem, zaraz spróbuje gdyż kąt COD=α

salamandra: sorki, nie zaznaczyłem go tutaj no ja próbowałem, ale nie wiedziałem co ze sobą przyrównać

a7: coś mi wyszło, zaraz sprawdzę i prześlę

a7: nie to był zły trop, jeszcze myślę...

Minto:

	1
V =		πr2*H
	3

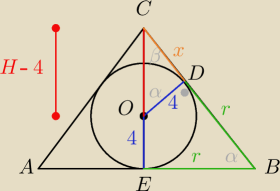
ΔODC jest prostokątny, zatem z tw. Pitagorasa (H−4)² = x²+4² x² = (H−4)²−4² = (H−8)H x = √H²−8H ΔODC ~ Δ BEC (kkk)

√H2−8H		H
	=
4		r

	4H
r =
	√H2−8H

	16		H2
V =		π*
	3		H−8

	16		2H(H−8)−H2
V'(H) =		π *		= 0 ⇔ H2−16H = 0 → H=16
	3		(H−8)2

trzeba dokończyć

a7:

4		r
	=
H−4		l

.l=√H²+r² podstawiamy l do pierwszego wyliczamy H i dalej jak zwykle

	8r2
H=
	r2−16

V(r)= itd.

salamandra: Dzięki Saizou!

	4		H−4
@a7, ja doszedłem do		=		i dalej już się tylko komplikowało
	r		√H2+r2

Minato:

a7: mi wyszło elegancko 4*l=r(H−4) l=√H²+r² 4*√H²+r²=r(H−4) 16H²+16r²=H²r²−8Hr²+16r² 16r² się redukuje H²(16−r²)+8Hr²=0 H²(r²−16)−8Hr²=0 H[H(r²−16)−8r²)=0

	8r2
H=
	r2−16

	1
V(r)=		πr2*H
	3

	1		8πr4
V(r)=		*
	3		r2−16

V'(r)=........itd.

salamandra: No to ja źle przyrównałem w sumie, jest różnica stosunek, który do którego weźmiemy, czy

	x		a
wyjdzie na to samo? Mam na myśli to, czy jest różnica, czy zapiszę		=		, czy
	y		b

	x		y
		=
	b		a

a7: jak przy wymnożeniu na ukos wychodzi to samo to jest ok, tutaj nie wychodzi to samo

Minato: Nie jest to samo, tożsame są zapisy

x		a
	=
y		b

y		b
	=
x		a

a		b
	=
x		y

x		y
	=
a		b

dla a, b, x, y ≠ 0

salamandra: o to mi chodziło