Trygonometria, ujemny cos Lukasz: Hej, mam pytanie co do ujemnych cos, sin etc. Bo słabo to rozumiem a nigdzie nie jest napisane w taki sposób żebym zrozumiał. Np. w zadaniu wychodzi mi cosβ = −1/2 Skąd mam teraz wiedzieć jaki on ma kąt? Skąd mam wiedzieć w której ćwiartce leży? A czasem nawet wychodzą jakieś brzydkie ułamki których nie ma w tablicy wartości tryg. Mam to zamieniać na radiany? Nie mam pojęcia jak odczytywać to z tablic matematycznych. Proszę o pomoc, bo nie chce stracić na maturze punktów za to że podałem zły kąt

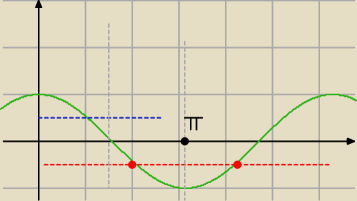
a7: cosx=−1/2 może są sprytniejsze sposoby, ale

	π
możesz to zrobić tak cosx=1/2 dla 60o czyli dla		to π/2 brakuje π/6 i −1/2 jest dla π/6
	3

po π/2 czyli dla 4/6π czyli 2π/3 następnie cosx jest równy −1/2 dla π+π/3= 4π/3, jeśli chodzi o brzydkie ułamki to obliczasz ich wartość i znajdujesz w tablicach,

Bleee: 'brzydkich' ułamków mieć nie będziesz na maturze. Zamiana na radianty to mocne przekombinowanie. Musisz przede wszystkim wiedzieć jak narysować wykres f(x) = sinx oraz f(x) = cosx na przedziale <0 ; 2π> I wtedy: I ćwiartka to −−− x∊ (0; π/2) II ćwiartka to −−− x∊ (π/2 ; π) III ćwiartka to −−− x∊ (π ; 3π/2) IV ćwiartka to −−− x∊ (3π/2 ; 2π) co do kątów ... wykorzystuje się wzory redukcyjne (powinny być na karcie wzorów ... jeżeli nie ma, to możesz jest 'wykombinować' na podstawie wykresu który MUSISZ potrafić narysować

Lukasz: @Bleee umieć umiem, ale raczej nie będę miał potrzeby rysowania wykresu bo są one w tablicach. Ale jak mam podane przedziały x∊ (0; π/2) etc. to jak mam −1/2 porównać dla którego przedziału pasuje bez zamiany na radiany ? skoro x = 1/2 a przedziały są w radianach

Jerzy: Opanuj wierszyk: W pierwszej wszystkie są dodatnie W drugiej tylko sinus W trzeciej tanges i cotanges A w czwartej cosinus Znając ten wierszyk, wyprowdzisz sobie szybko każdy wzór redukcyjny.

Lukasz: Znaczy wierszyk znam, tylko probllem jest w tym, że nie wiem do której ćwiartki należy liczba

a7: no to podaj kilka przykładów, to będzie łatwiej

Jerzy: Podaj konkretny przykład.

Lukasz: np tak jak mam cosβ = −1/2 to ja to bym zamieniał na −^π₃ i odejmował od π i wtedy zobaczyć na wykresie że cos nalezy do przedzialu π/2 ; 3/2π ale nie wiem juz czy to jest poprawnie, bo Bleee pisał ze zamiana na radiany to przekombinowanie

Jerzy: cosx = −1/2 ⇔ cosx = − cos(π/3) ⇔ cosx = cos(π − π/3) ⇔ x = 2/3π + 2kπ lub x = −2/3π + 2kπ

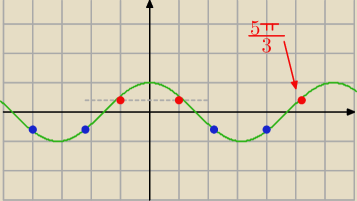
a7: 14:32 wiemy, że cosinus się powtarza co 2π czyli mamy −π/3 i dodajemy 2π i mamy 5π/3 (tylko, że zauważ, że to jest 1/2) dla −1/2 jest tak jak pisałam 14:06

Lukasz: No to jako przykład niech będzie cosα = −√3/2 Ja nie mówię o liczeniu x w równaniach. Tylko Obliczanie jaki kąt jest dla ujemnych cos, sin itp. Jak np mam cos = −√3/2 cosα = −π/6 czyli cosα leży w 1 ćwiartce?

Jerzy: Jeśli cosα = − √3/2 , to α leży w drugiej lub trzeciej ćwiartce ( to wynika z "wierszyka", bo tam cosinus ma wartości ujemne)

Lukasz: odczytywanie jaki x jest dla jakiej α jest dla mnie zrozumiałe ale jaki kąt jest dla danego cos to nie rozumiem tego

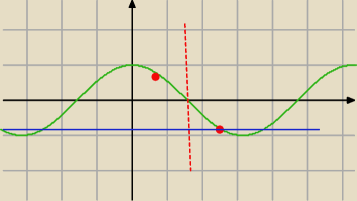
a7: to możesz to zrobić tak cos30=√3/2 czyli π/6 czyli tu masz x=π/2 plus 2π/6 czyli x=5π/6 czyli 150^o czyli x leży w drugiej ćwiartce

Lukasz: Powoli zaczynam rozumieć. No a jak już wiem do której ćwiartki należy cos to skąd mam wiedzieć który wzór wykorzystać bo są 2 dla ujemnego cos −cosα = cos(180stopni − α) i −cosα = cos(180stopni + α)

Lukasz: a7: a czy x nie moze też być x=7π/6 ? wtedy też przyjmuje wartość −√3/2 chyba?

Jerzy: @Lukasz, jest nieskończenie wiele kątów, dla których cosα = −√3/2

Jerzy: 15:14, to oznacza ,że w przediale [0,2π] są tylko dwa takie kąty

Lukasz: @Jerzy tak racja, ale biorąc pod uwagę że wyliczam sobie że α=5π/6 v α=7/6π to powinny być wciąż takie same kąty? i jak mam zamienić te radiany na stopnie? i skąd mam wiedzieć który wzór użyć? pytanie z 15:14

a7: 15:20 tak masz rację to czyli wtedy nie wiadomo czy druga czy trzecia ćwiartka, jak tylko to jest podane, ale wiadomo, że nie pierwsza i nie czwarta , a to też jest czasem wystarczające do zadania

Lukasz: jak podstawiam pod 1 wzór −cosα = cos(180stopni − α) α=5π/6 ⇒ cos(2π−5/6π) = cos 7/6π = 90 + 30 = 120? α=7/6π ⇒ cos(2π−7/6π)= cos 5/6π ⇒ nie wiem jak to zliczyć 2 wzór −cosα = cos(180stopni + α) α=5π/6 ⇒ cos(2π + 5/6π) = cos 17/6π ⇒ α=7/6π ⇒ cos(2π + 7/6π) = cos 19/6π ⇒

a7: no to jeśli chodzi o 15:33 to wiesz, że 5π/6 to 150^o czyli cos 150=cos(90+60)=−sin60 wg mnie , o ile dobrze pamiętam, to co podstawiasz do wzoru już musi być mniejsze niż 90^o czyli niż π/4

a7: 90 tj. π/2

Lukasz: no a jak wyliczyć ile ma 5/6π ? bo właśnie próbowalem to podstawić do wzoru α=5π/6 ⇒ cos(2π−5/6π) = cos 7/6π = 90 + 30 = 120 i wyszlo mi 120

Lukasz: to 5/6π > 90 więc co mam zrobić z czymś takim?

Jerzy: Poczytaj to, może zrozumiesz "o co biega". https://www.medianauka.pl/wzory-redukcyjne

a7:

	√3
15:36 Ci napisałam, że jak masz 5π/6 to to jest −sin60 czyli to jest −
	2

a7: używasz tego wzoru ile masz stopni poniżej 90−ciu to znaczy jak masz 60 i chcesz sinus to masz albo od razu √3/2 z tablic albo możesz się bawić jak to jest potrzebne i zamienić sin(90−30)=cos30=√3/2 wyjdzie zawsze na to samo jeśli tylko poprawnie użyjesz wzorów

Lukasz: No zamiana sin na cos jasna, tylko tak jak pisałem, nie wiem jeszcze tylko jak zamienić 5/6π na 150 stopni? jak to się stało? pytanie z 15:38

a7: π=180

a7: https://matematykaszkolna.pl/strona/2893.html

Lukasz: Aaaa, rzeczywiście. To zmienia postać rzeczy już. Czyli to wychodzi tak (biorę pod uwagę że nie odejmuje większego kąta niż 90) cos 5/6π = cos(π−1/6π) = −cos 1/6π = √3/2 = 30

a7: 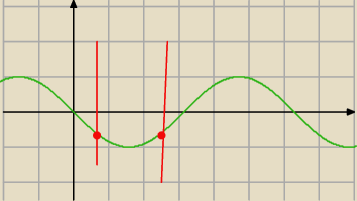https://matematykaszkolna.pl/strona/430.html −cos(π/6)=−√3/2≈−0,86602 chyba raczej chodzi Ci o to, żeby wyszło na plusie trzeba zrobić cos(π/2+π/3)=−sin(π/3)=−√3{2} nijak z tego nie wyjdzie plus musisz gdy już wiesz, że to jest −√3{2} dla −sin(π/3) to możesz też narysować −sinx i też odczytać z wykresy −sinx

Lukasz: Oczywiście tam jest błąd, ma być minus. Zależy mi tylko na tym żeby wiedzieć jaki jest kąt dla wartości 5/6π

Lukasz: ale wydaje mi się że już rozumiem. I jak mam te −cos 1/6π to podstawiam cos(180−α)= −cosα cos(180−30)=150

Jerzy: Chyba nie rozróżniasz wartości funkcji (liczby), od argumentu (kąta) Co to jest cos(180 − 30) = 150 ?

Lukasz: jeżeli −cos 1/6π to α w tym przypadku to 1/6π ⇒ α=30stopni Wstawiam na wzór −cosα=cos(180−α) ⇒ cos(180stopni − 30stopni) = cos150 ?

a7:

	5
5π/6=		*180o=150o
	6

π
	=30o
6

a7: 16:40 źle

a7: cos(π/6)=1/2 −cos(π/6)=−1/2

a7: Łukasz, może pokaż konkretne zadanie, gdzie to jest zastosowane, bo tak to trochę nie wiadomo, o co Ci chodzi

Jerzy: Co źle ? cos150 = cos(180 − 30) = −cos30 = − cos(π/6)

Lukasz: Okej, zaraz znajde takie zadanie i tu podeślę.

a7: no to jak jednak dobrze, to ok, ja w takim razie cofam, jednak podtrzymuję, że lepiej byłoby mieć konkretne zadanie i tłumaczyć

a7: ok

Lukasz: Wysokość ostrosłupa prawidłowego czworokątnego jest równa 2, a jego krawedz podstawy ma dl 4. Oblicz miarę kąta między sąsiednimi ścianami bocznymi tego ostroslupa. Z tego wyszło właśnie cosα = −1/2 α=√3/3 −cos √3/3 = cos(180stopni − 60stopni) = 120stopni

Lukasz: Albo jeszcze inne zadanie, z tego forum, tylko tu cos wychodzi troche "brzydszy": dany jest ostrosłup prawidłowy czworokątny w którym wszystkie krawędzie maja rowna dlugosc, oblicz kosinus tego kąta odp wychodzi cosα = −1/3

Lukasz: i gdybym chciał zamienić −1/3 na kąt : α≈71stopni −cos71 = cos(180−71) = 109stopni?

a7: 17:27 https://matematykaszkolna.pl/forum/188071.html

a7: 17:31 https://matematykaszkolna.pl/strona/2045.html

a7: dobra rozumiem, jak cosinus w takim zadaniach wychodzi ujemny to znaczy, że kąt jest większy niż 90

a7: 17:35 akurat nie pamiętam bym takim sposobem do tego podchodziła, ale wychodzi na to, że jest to również poprawne

a7:

Lukasz: no te pierwsze zadanie to zrobiłem wczesniej i nie umiałem tyko zamienić ujemnego cos na kąt. Okej, czyli jeśli mam takie zadania, to trzeba założyć że kąt pomiędzy ścianami nie może być większy niż 180 i jest większy niż 90 stopni ?

Lukasz: jeśli oczywiście cos wyszedłby ujemny*

a7: 17:47 tak, jeśli cosinus wyjdzie ujemny, jeśli dodatni to normalnie będzie to kąt ostry

a7: 17:47 tak, tak właśnie

Lukasz: Dobra, to ja już to w miare rozumiem, jesli cos nie bedzie jasnego jakis przyklad, zadanie, to napisze tutaj. I dziękuje ogromnie za pomoc i cierpliwość do mnie na prawdę, bo chcę to umieć i sam bym tego nie zrozumiał

a7: