Oblicz miarę kąta między sąsiednimi ścianami bocznymi ostrosłupa. janek: Witam, Wysokość ostrosłupa prawidłowego czworokątnego jest równa 2 a krawędź podstawy ma długość 4, oblicz miarę kąta między sąsiednimi ścianami bocznymi tego ostrosłupa. chciałem obliczyć to z twierdzenia cosinusów ale wychodzi mi 2/3 : obliczyłem wysokość ściany bocznej, i długość krawędzi bocznej. Następnie ze wzoru na pole trójkąta obliczyłem ramię kąta dwuściennego ( jeżeli tak mogę to pisać ) i wszystko podstawiłem do wzoru cosinusów. Proszę o pomoc z jakimś opisem co z czego wynika.

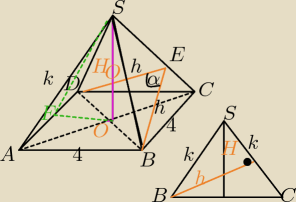
Mila: DB=4√2 WΔSOF: SF=2√2=H W ΔSOB: z tw. Pitagorasa: k²=2²+(2√2)²⇔k²=4+8=12⇔k=2√3

	1
PΔBCS=		*4*2√2=4√2
	2

	1
PΔBCS=		*2√3*h⇔√3*h=4√2
	2

	4√2
h=
	√3

W ΔDEB:

	4√2		4√2		4√2
(4√2)2=(		)2+(		)2−2*(		)2*cosα
	√3		√3		√3

	32		32		32
32=		+		−2*		cosα
	3		3		3

	64		64
32=		−		cosα /*3
	3		3

96=64−64cosα 32=−64cosα

	1
cosα=−		⇔α=120o
	2

Masz odpowiedź?

janek: tak zgadza się, dzięki

Mila:

janek: zrobiłem błąd rachunkowy dlatego nie wyszło