matura Andrzej: To zadanie było na maturze w 1995 (chyba ) roku w województwie radomskim: https://matematykaszkolna.pl/forum/402256.html

23: Ale K jest środkiem boku wg ciebie na rysunku Mili ?

Andrzej: A czemu tego wątku nie ma na stronie forum?

23: nie rozumiem. Jak klikam w twoj link jestem w watku.

Andrzej: Też widzę dziwna sytuacja

Andrzej: Już jest

Mila: K nie jest środkiem krawędzi. Wieczorem narysuję jeszcze raz i policzę. Tymczasem podpowiedź:

	a
|AP|=		i ΔADE jest Δ równobocznym:
	2

ΔADE∼ΔABC

a		b√3
	=
2		2

	a
b=
	√3

	1
skala podobieństwa k=
	√3

23: Mila myślę że już jest wieczór czekamy Ja coś czuję że źle zaznaczałem "przechodząca w odległości 0,5a od jednej z tych krawędzi" gdzie jest to 0,5a na rysunku ?

Mila:

	a3√2
VABCS=
	12

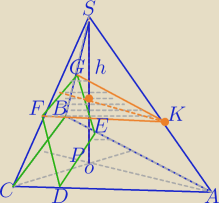
a− krawędź czworościanu foremnego H− wysokość czworościanu ABCS

	a
|AP|=
	2

ΔADE− trójkąt równoboczny o boku b

	a		b√3
|AP|=		=
	2		2

	a
a=b√3⇔b=
	√3

ΔDEA≡ΔFKG

	b		a   √3		1		√3
ΔDEA∼ΔABC w skali k=		=		=		=
	a		a		√3		3

2)Ostrosłup FKGS∼

	√3		a3√2		a3√2
VFKGS=(		)3*		=
	3		12		12

	√3
3) h=		*H
	3

h_g− wysokość graniastosłupa

	√3		√3		3−√3
hg=H−		*H=H*(1−		)=H*
	3		3		3

	√3		a2√3		a√6		3−√3
Vg=(		)2*		*		*
	3		4		3		3

	a3*(3√2−√6)
Vg=
	108

Ostatnio mam mało czasu, w sobotę spojrzę tu jeszcze raz i przeliczę spokojnie. Czekaj cierpliwie, chyba to nie jest pilne?

klan: Czy V_g to objetość jednej z tych dwóch figur?

Mila: V_g to objętość graniastosłupa DAEFKG, z tym , że nie mam pewności, czy dobrze ustalone:

	a
|AP|=		.
	2

Poczekamy na Bogdana i jego opinię.

Akcent: To chyba za trudne na mature

Mila: Oczywiście. Skąd macie to zadanie? Podam podobne zadanie, ale łatwiejsze (nieco), jeśli to Cię Akcent interesuje. Napisz.

Akcent: U góry napiasne ze z matury

Mila: Rozwiąż takie zadanie : W czworościanie o podstawie ABC i wierzchołku D poprowadzono płaszczyznę przechodzącą przez środki krawędzi AB, BD, CD. Płaszczyzna ta dzieli czworościan na dwie bryły. wiedząc, że objętość czworościanu ABCD wynosi V, wyznacz objętości tych brył.

ABC: Mila to jest oryginalne zadanie maturalne : https://zapodaj.net/c22bb34300931.jpg.html wkleić wam rozwiązanie?

Mila: ABC, chcę wiedzieć , gdzie jest odległość 0.5a na moim rysunku. 23:29 Będę wdzięczna, coś mnie zawodzi wyobraźnia przestrzenna ( nęka mnie ząb).

ABC: są dwie strony, to jest zadanie 4b z gwiazdką , podpunkt a był łatwiejszy https://zapodaj.net/0e579397a7577.jpg.html https://zapodaj.net/0872a0254d4b8.jpg.html

Mila: Dzięki ABC, przeanalizuję

a7: fajnie ja też byłam ciekawa jak to w końcu jest

a7: Dziękuję ABC!

ABC: macie szczęście że kupiłem II wydanie z aneksem na pchlim targu od pijaka za 3 zł , w I wydaniu tych zadań nie było

Mila: Witaj a7, mocno się napracowałaś Zobacz, gdzie się pomyliłaś.

	1
Rozwiąż zadanie , które tu podałam 18:55 . Skala k=
	2

a7: Witaj Milu, bardzo lubię takie bawienie się w rozwiązywanie zadań dla sportu ( z tymże to mnie przerosło, chociaż zauważyłam, że część punktów bym dostała a to było z gwiazdką*, więc i tak jest nieźle), do zadania z 18:55 widziałam chyba rozwiązanie w necie lub tutaj, więc chyba nie jest takim wyzwaniem niech maturzyści się pomęczą, ale jeżeli chcesz, żeby było w zasobach forum to spróbuję je zrobić, bo właśnie szukałam i już nie widzę, daj proszę znać lub niech da znać kto się podejmuje próby

Mila: a7 Ja już wiem, gdzie popełniłam błąd, wczoraj późnym wieczorem, wpadłam na pomysł, że trzeba

	a
wziąć pod uwagę odległość krawędzi skośnych i tam ustalić odległość		.
	2

Teraz to proste. Moje wcześniejsze rozwiązanie dobre, gdy wiadomo w jakim stosunku przecięte są krawędzie. Miałam też zamiar skorzystać z geometrii analitycznej w R3. Dobrze, że ABC przysłał nam wspaniały materiał.

a7: Ja dokładnie nie wiem, gdzie jest mój błąd, ale zauważyłam, że też jest zrobione z dwoma ostrosłupami "bocznymi" jak w jednej z moich przymiarek

kurdek: Czyli z tym klinem podamym w linku było dobrze......