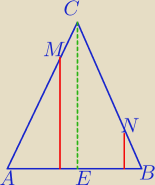
planimetria jaros: Dany jest trójkąt równoramienny ABC, w którym |AC| = |BC|. Na ramieniu AC tego trójkąta wybrano punkt M (M ≠ A i M ≠ C ), a na ramieniu BC wybrano punkt N, w taki sposób, że |AM| = |CN|. Przez punkty M i N poprowadzono proste prostopadłe do podstawy AB tego trójkąta,

	1
które wyznaczają na niej punkty S i T. Udowodnij, że |ST| =		|AB|.
	2

	AM		IAMI
1) ΔASM ~ ΔAEC (kkk) w skali		, więc IASI =		* IAEI
	AC		IACI

	BN		BN		BC − CN
2) ΔBTN ~ ΔBEC (kkk) w skali		więc IBTI = BE *		= BE *		=
	BC		BC		BC

	AE		1
i teraz moje pytanie, skąd to się równa (1 −		) * IAEI = IAEI =		IABI
	AC		2

jaros:

	AM
Tam w nawiase powinno być 1 −
	AC

jaros: A dobra nie ważne

Qulka: https://matematykaszkolna.pl/forum/401806.html

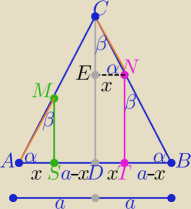Eta: |AB|=2a ΔASM ≡ ΔCEN z cechy (kbk) to |AS|=|DT|=x więc |ST|=a−x+x= a

	1
|ST|=		|AB|
	2

=========== c.n.w.