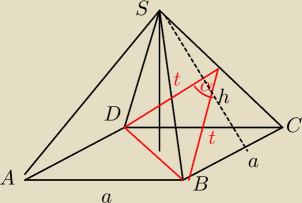
stereometria salamandra: W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa. Pp=a²

	1
PBSC=		a2
	2

	a*h
PBSC=
	2

1		a*h
	a2=		/ * 2
2		2

a²=a*h h=a

	1
SC2=		a2+a2
	4

	5
SC2=		a2
	4

	a√5
SC=
	2

Pole na drugi sposób:

1		a√5   t*   2
	a2=		/ *2
2		2

	a√5
a2=t*
	2

	a2		2a√5
t=		⇒ t=
	a√5   2		5

z tw. cosinusów:

	2a√5		2a√5		2a√5		2a√5
(a√2)2=(		)2+(		)2−2*(		)2*(		)2*cosα
	5		5		5		5

	20a2		20a2		20a2
2a2=		+		−2(		)*cosα
	25		25		25

	40a2		40a2
2a2=		−		*cosα
	25		25

50a2−40a2   25
	=cosα
40a2   −   25

	10a2		25		1
cosα=		*		=−
	25		−40a2		4

ok?

Eta:

salamandra: No to w takim razie dobranoc, ostatnie, optymalizacyjne na rano

Eta: https://matematykaszkolna.pl/forum/402246.html podobne Dobranoc

Eta: Rozwalisz maturę na 200%

salamandra: Wiem, że podobne, właśnie miałem tam wcześniej napisać, że czeka mnie właśnie to zadanie, ale dopiero później doczytałem, że tutaj pola są danymi

salamandra: Eta.... jestem realistą, z 70% będę w miarę zadowolony

Eta: 100% na bank

salamandra: Z podstawy

Eta: Obstawiam 100% i 100%

Eta: Jak to dobrze,że tu do nas trafiłeś, fajnie się z Tobą pracuje

salamandra: To ja nie obstawię, ale powiem fakt, że gdyby nie Wy, to nie byłoby nawet szans na 50%

Eta: Będzie dobrze i tak trzymaj !

salamandra: Dziękuję za miłe słowa, dużo bym dał, żeby Twoje przewidywania się spełniły