ostrosłup julcia: W prawidłowym ostrosłupie czworokątnym krawędź boczna o długości 10 tworzy z płaszczyzną podstway kąt 60°. Oblicz cosinus kąta między dwiema kolejnymi ścianami bocznymi ostrosłupa.

Eta:

	1
cosα= −
	7

@julcia Czekam, bo może któryś z maturzystów : salamandra , Patryk ,..... Ci pomogą ?

Eta: Jeszcze i fil

salamandra:

	a√2
cos60=
	10

1		a√2
	=
2		10

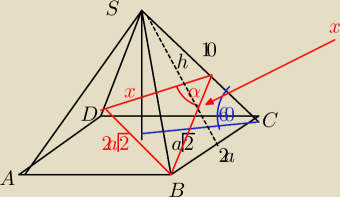
10=2a√2 10√2=4a 5√2=2a

	5√2
a=
	2

z tw. Pitagorasa w BCS:

25
	+h2=100
2

	5√14
h=
	2

	1
P=		*2a*h
	2

	5√14		1		25√7
P=5√2*		*		=
	2		2		2

Pole BCS na drugi sposób:

	1
P=10*x*
	2

25√7		1
	=10*x*
2		2

	5√7
x=
	2

Z tw. cosinusów w czerwonym:

	5√7		5√7		5√7
100=(		)2+(		)2−2*(		)2*cosα
	2		2		2

	350		175
100=		−		*cosα / * 4
	4		2

400=350−350*cosα

	50		1
cosα=		=−
	−350		7

fil: @salamandra ty chyba jestes pracoholikiem

salamandra: Nie większym niż ty

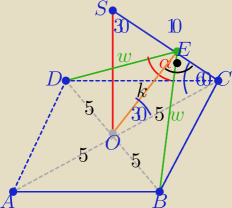
Eta: Strasznie się oliczyłeś ( jak z czasem na maturze będzie ? Ładnie,że podjąłeś wyzwanie To ja tak: d_p=10 z "ekierki" OCS

	5√3
k=		−−− z "ekierki" OCE
	2

	175
to w ΔOBE : w2=52+k2 =...=
	4

z tw. cosinusów w ΔBED : cosα= U{w²+w²−d²}{2w*w

	d2		200		25
cosα= 1−		= 1−		= −
	2w2		175		175

	1
cosα= −
	7

==========

Eta: Poprawiam zapis:

	w2+w2−d2
cosα=
	2w*w

Eta: A Ty fil ? ... leniuchem

salamandra: zrobiłem najszybciej jak umiem

Eta:

kurdek: https://matematykaszkolna.pl/forum/402256.html

fil: @Eta ja juz odpoczywam przed matura

salamandra: Nieładnie Etę oszukiwać

ICSP: i dlatego planimetrię, stereometrię zostawia się na sam koniec. No może przed zadaniami dowodowymi i prawdopodobieństwem.

Eta: Jak wrzucisz zadanko ..... nie odpowiem

fil: a, moze jeszcze jakies zadanko sie zrobi