planimetria Chila: Punkt A należy do obszaru kąta o mierze 60 stopni. Odległość punktu A od ramion kąta są równe a = 2 b = √3−1. Oblicz odległość punktu A od wierzchołka kąta.

Mila: 401920

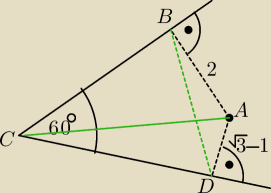
getin: Twierdzenie cosinusów dla ΔABD |BD|² = |AB|² + |AD|² − 2*|AB|*|AD|*cos120^o

	1
|BD|2 = 22 + (√3−1)2 − 2*2*(√3−1)*(−		)
	2

|BD|² = 6 |BD| = √6 Na czworokącie ABCD można opisać okrąg, bo suma miar kątów ABC i ACD jest równa sumie miar kątów BAD i BCD Z tw. sinusów w ΔABD

|BD|
	= 2R
sin120o

gdzie R − promień okręgu opisanego na ΔABD

√6
	= 2R
√3   2

2√2 = 2R |AC| = 2√2