| 1 | 10 | |||
∡P20P13P6 = | *360o* | = 75o | ||
| 2 | 24 |
| 1 | 4 | |||
∡P13P20P9 = | *360o* | = 30o | ||
| 2 | 24 |
 Wniosek z tego, że ...
Wniosek z tego, że ... 
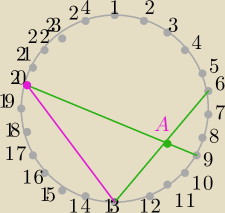 360:24=15
∡AP20=30 (kąt wpisany będący połową kąta środkowego opartego na łuku P9P13)
∡AP13=75 (kąt wpisany będący połową kąta środkowego opartego na łuku P6P20)
∡P20AP13=180−30−75=75 (suma miar kątów w trójkącie wynosi 180, odejmujemy obliczone
kąty)
∡P20AP13=∡AP13P20 czyli trójkąt AP20P13 jest równoramienny, c.n.w.
360:24=15
∡AP20=30 (kąt wpisany będący połową kąta środkowego opartego na łuku P9P13)
∡AP13=75 (kąt wpisany będący połową kąta środkowego opartego na łuku P6P20)
∡P20AP13=180−30−75=75 (suma miar kątów w trójkącie wynosi 180, odejmujemy obliczone
kąty)
∡P20AP13=∡AP13P20 czyli trójkąt AP20P13 jest równoramienny, c.n.w.