pochodna hania: Dziedziną funkcji f jest przedział (−8;11). Funkcja f jest ciągła oraz: f ' (x) > 0 ⟺ x ∈ (−8,−3) ∪ (−3,4) ∪ (7,11) f ' (x) < 0 ⟺ x ∈ (4,7) f ' (x) = 0 ⟺ (x = −3 v x = 4) W punkcie x=7 pochodna funkcji f nie istnieje. Do wykresu funkcji f należą punkty (2,5) i (7,5). Na podstawie powyższych danych: a) Wyznacz punkty, w których funkcja f ma ekstrema lokalne. b) Uporządkuj od najmniejszej do największej liczby: f(1), f(−3), f(6), f(−7). Odpowiedź uzasadnij. jedynie widze ze w −3 nie ma ekstremum, a w 4 ma maksimum, czy ktos moglby mi objasnic, ale tak dosc lopatologicznie, co sie dzieje z ta funkcja w 7 ze nie istnije pochodna, a funkcja jest ciagla i przyjmuje wartosc 5

a7: https://matematykaszkolna.pl/forum/400161.html

hania: kurde, dalej nie rozumiem czemu nie ma w tym punkcie pochodnej. ale dzieki

a7: tutaj teoria na temat monotoniczności http://matematykadlastudenta.pl/strona/198.html a jeśli chodzi o ten punkt x₀=7 to znaczy, że funkcja jest w tym punkcie "ostra" (patrz rysunek) wtedy jest ciągła, a pochodnej nie ma

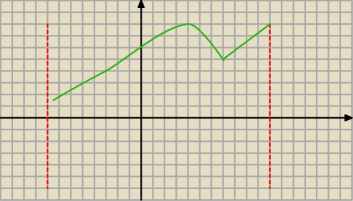
a7: PS> oczywiście rysunek jest poglądowy (nie uwzględniłam punktu (2,5)