pochodna mr. t: Dziedziną funkcji f jest przedział (−8, 11). Funkcja f jest ciągła oraz f'(x)>0 ⇔ x∊(−8;−3) u (−3;4) u (7;11), f'(x)<0 ⇔ x∊(4;7) , f'(x)=0⇔(x=−3 v x=4) W punkcie x = 7 pochodna funkcji f nie istnieje. Do wykresu funkcji f należą punkty (2, 5) i (7, 5). Na podstawie powyższych danych: a) wyznacz punkty, w których funkcja f ma ekstrema lokalne b) uporządkuj od najmniejszej do najwiekszej liczby: f(1), f(−3), f(6), f(−7) Wiem, że na pewno jedno ekstremum znajduje się w 4, co do drugiego mam watpliwosci czy jest w 7, tylko dla x=7 pochodna nie istnieje Nie wiem czy jedno wyklucza drugie... co do podpunktu b, nie mam pojecia jak sie za niego zabrać

wredulus_pospolitus: Jeśli chodzi o ekstrema to: w x = −3 nie ma ekstremum (jest punkt przegięcia −−−> patrz wykres g(x) = x³ dla okolic x=0 ) w x = 4 masz maksimum lokalne w x = 7 masz minimum lokalne −−− jednak tutaj zmiana monotoniczności funkcji musi być 'nagła' (patrz h(x) = |x| w okolicach punktu x = 0) Uwaga do punktu 7 −−− tu musi być ekstremum ze względu na to, że mamy podane, że funkcja f(x) jest CIĄGŁA więc nie ma możliwości abyśmy mieli w tym miejscu 'uskok'.

wredulus_pospolitus: co do (b) wiemy, że funkcja rośnie w przedziale (−8 ; 4) (w −3 jest punkt przegięcia, ale on nie zmienia monotoniczności samej funkcji). więc ... f(−7) < f(−3) < f(1) wiemy, że f(2) = 5 .... a przecież f(1) < f(2) = 5 wiemy także, że f(7) = 5 ... a przecież 5 = f(7) < f(6) (bo funkcja maleje na przedziale (4,7) stąd mamy: f(−7) < f(−3) < f(1) < 5 < f(6)

mr. t: jedno pytaie do podpunktu a, czy informacja, iż nie ma pochodnej dla x=7 nie wyklucza istnienia ekstremum?

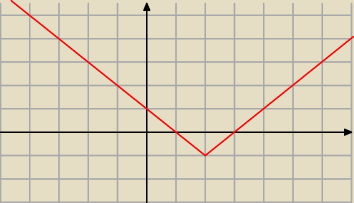
wredulus_pospolitus: Odpowiem pytaniem (i wykresem) na pytanie Czy funkcja f(x) = |x−2| − 1 posiada minimum lokalne w x=2 Reasumując: dzięki pochodnej wiemy czy w danym punkcie jest czy nie ma ekstremum, ale nie istnienie pochodnej w danym punkcie nie przesądza o tym 'co się dzieje z funkcją' w tymże punkcie.

wredulus_pospolitus: mr t: gdyby w x=7 NIE BYŁO ekstremum to powstają następujące problemy: 1) W jaki sposób funkcja z malejącej zmienia się na rosnącą (monotoniczność) Odpowiedź: no bo jest 'skok' wartości funkcji (jedyna możliwość w momencie w którym x=7 należy do dziedziny funkcji) 2) Ale jak możliwy jest 'skok' wartości funkcji w momencie w którym ma być ona ciągła? Odpowiedź: Jest to niemożliwe.

mr. t: super, dzieki wielkie