geometria analityczna salamandra: Okrąg o równaniu o: x²+2x+y²+2y=14 jest styczny do prostych k: 4y−3x−19=0 i l: 4y+3x+27=0 w punktach K i L odpowednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu o, prostych k i l oraz nie przechodzą przez punkty K i L Wstawiam zdjęcie, co udało mi się zrobić oraz podgląd z Geogebry jak podstawiłem dane. Brakuje mi pomysłu jak wyznaczyć równania tych okręgów.

	23
Wyznaczyłem jeszcze punkt M (punkt przecięcia prostych K i L), M=(−		, −1)
	3

https://imgur.com/a/4nsyoCb

Qulka: chyba to zadanie już było na forum

salamandra: ja nie jestem dobry w szukaniu tutaj

Qulka: może że ich środek leży na prostej MS i odległość od k =r a od S=r+4

Qulka: albo https://matematykaszkolna.pl/forum/401689.html

an: A na Geogebrze co masz napisane

salamandra: Wysłałem screena co zaznaczyłem na geogebrze

an: na geogebrze wpisałeś dane z zadania i tyle, opisy p/n są zbyt skomplikowane i nie bardzo wiadomo czego dotyczą zrób rysunek zaznacz co liczysz i po co.

salamandra: Mówię, że wyznaczyłem współrzędne punktów styczności K i L, oraz współrzędne punktu przecięcia prostych podanych w zadaniu "M". Nie wiem jak się zabrać do tych okręgów. No i nie napisałem jeszcze, że S=(−1,−1) i r=4

an: ale czy chociaż przypuszczasz jak usytuowane są te okręgi

salamandra: Tak, wiem jak są usytuowane, ale nie potrafię dojść do rozwiązania

an: dobra nie chce mi się dalej z Tobą droczyć, czy widziałeś to co podała Qulka

an: To widziałeś czy nie ?

Eta:

Mila: salamandra Masz odpowiedź? Eta liczyłaś?

salamandra: ja policzyłem− pierwszy (mniejszy okrąg): (x+6)²+(y+1)²=1 drugi (większy): (x−19)²+(y+1)²=16

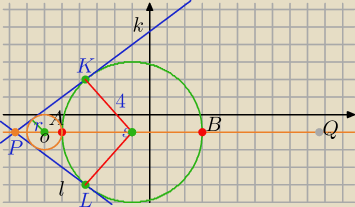
Mila: o: x²+2x+y²+2y=14 jest styczny do prostych k: 4y−3x−19=0 i l: 4y+3x+27=0 o: (x+1)²+(y+1)²=16 P=(−23}{3},−1) 1) Środki okręgów stycznych do ramion kąta KPL leżą na dwusiecznej tego kąta , okręgi mają być styczne też do danego okręgu zewnętrznie to jeden będzie położony na lewo od punktu A, a drugi na prawo od punktu B A=(−5,−1), B=(3,−1) O=(x₁,−1)),x₁<−5 |AO|=√(x₁+5)²+(−1+1)²=|x₁+5|

	|4*(−1)−3x1−19		|4*(−1)−3x1−19|
d(O, k)=		=
	√42+32		5

	|−4−3x1−19|
|(x1+5)|=
	5

5(x₁+5)=|3x₁+23| x₁=−6 lub x₁=−1∉D r=1 , O=(−6,−1) (x+6)²+(y+1)²=1 ========== 2) Q=(q,−1), q>3, B=(3,−1) |BQ|=√(q−3)²+(−1+1)²=|q−3| d(Q,k)=d(Q,l)=|BQ| licz dalej sam, posprawdzaj rachunki.

Mila: Zgadza się z moimi rachunkami, chociaż wydawało mi się, że po prawej powinno być więcej okręgów.

salamandra: Chyba nie jest to możliwe, bo nie mógłby być styczny do wyjściowego okręgu i prostych? dziękuję za przeliczenie. Rozumiem, że to, że przesuwasz o cztery jednostki, ponieważ punkt S i P leżą na tej samej współrzędnej "y" i można się zająć tylko "x"?

Mila: Korzystam z definicji odległości punktów A i O oraz wzoru na odległość punktu od prostej. Przeczytaj komentarz w punkcie 1.

Eta: Hej Mila Ja liczyłam z podobieństwa trójkątów S₁(−6,−1) r₁=1 i S₂(19,−1) r₂=16 o₁ : (x+6)²+(y+1)²=1 o₂: (x−19)²+y(+1)²= 256

salamandra: Tak, ja rozumiem, ale mam na myśli to, że jakby rzędna P była inna niż S, to wtedy nie moglibyśmy założyć, że dla S1 i S2 to również −1?

wredulus_pospolitus: ale S₁ i S₂ leżałyby na prostej przechodzącej przez P i S

wredulus_pospolitus: więc znając odległość od punktu P do punktu S₁ i wiedząc na jakiej prostej leży ... wyznaczasz współrzędne punktu S₁

salamandra: Tak, chodziło mi tylko o to, że tutaj mieliśmy ułatwienie, że musieliśmy się zajmować tylko współrzędną "x"

Mila: Dzięki Eta, też liczyłam z podobieństwa, wydawało mi się, że jest więcej rozwiązań, ( po prawej) dlatego odwołałam się do podanego sposobu.