Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątn michał: Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną (zobacz rysunek).

michał: Jaka powinna być długość tej przekątnej, aby pole powierzchni tego rombu było największe możliwe?

michał: https://imgur.com/a/0gtDMgC

fil: czyste zadanie optymalizacyjne

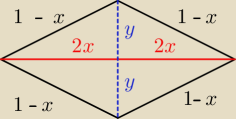
wredulus_pospolitus: zał. 4x ∊ ( 0 ; 4/3 ) −−> x ∊ ( 0 ; 1/3 ) y² + (2x)² = (1−x)² wyznacz 'y'

	2y*4x
Prombu =
	2

podstawiasz wyznaczony 'y' ... funkcja jednej zmiennej ... szukasz maksimum wyznaczasz ile równe jest 4x = ...

Poprostupatryk: wredus a czemu zaznaczyłeś krawędź rombu jako 1− x.

wredulus_pospolitus: 4 krawędzie + przekątna mają długość 4 przekątną oznaczyłem jako długość 4x ... więc 4 krawędzie mają długość 4 − 4x

	4 − 4x
więc jedna krawędź ma długość		= 1 − x
	4

wredulus_pospolitus: specjalnie tak oznaczyłem przekątną ... aby nie mieć ułamków

Poprostupatryk: Bardzo mądrze, dzięki

wredulus_pospolitus: zastanów się przez moment skąd mam założenie, że 4x ∊ ( 0 ; 4/3 )

salamandra: https://matematykaszkolna.pl/forum/400836.html

wredulus_pospolitus: @salamandra −−− a Ty jak zwykle utrudniałeś sobie życie z tym wzorem na pole rombu

Poprostupatryk: no rozumiem już wredusku, mam tylko wątpliwości przy przejściu: P(x) = √−8x³+4x² ... P'(x) = −24x²+8x W wykropkowanych miejscach nie wiem co napisać. Czy może, że "...√−8x³+4x² jest tak samo monotoniczne jak −8x³+4x². Od teraz będę badał funkcję √−8x³+4x²... ?"

salamandra: @wredulus... to było ponad dwa tygodnie temu, już bym tego nie zrobił

wredulus_pospolitus: dziwna funkcja P(x) Ci wyszła y² = 1 − 2x − 3x²

	(P(x))2
polecałbym liczyć pochodną z funkcji:
	16