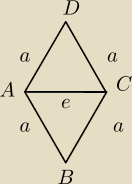
optymalizacja salamandra: Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną (zobacz rysunek).

	4−e
4a+e=4 ⇒ a=
	4

w ΔADC

	4−e   4−e   + +e 4   4		4+e
p (połowa obwodu) =		=
	2		4

	4+e		4+e		4−e		4+e		4−e		4+e
P=√		(		−		)(		−		)(		−e) =
	4		4		4		4		4		4

	−3e4−8e3+16e2
√
	64

Pole rombu: 2*P f(e)=−3e⁴−8e³+16e² f'(e)=−12e³−24e²+32e f'(e)=0 ⇔ −12e³−24e²+32e

	−3+√33		−3−√33
e=0 v e=		v e=
	3		3

	−3+√33
funkcja jest określona dla e>0, więc max będzie dla e=
	3

Brzydka liczba, więc zapewne się gdzieś pomyliłem albo źle do tego podszedłem?

Jerzy:

	2a + e
W trójkącie ADC połowa obwodu p =
	2

salamandra: No to dobrze mam połowę obwodu, a dalej?

Jerzy: A do czego ci potrzena połowa obwodu.Wyznacz drugą przekatną, wyznacz pole rombu jako połowę iloczynu przkatnych ( jako funkja e) i optymalizuj.

salamandra: liczyłem z Herona, po to mi była potrzebna połowa obwodu, tylko ten pomysł mi przyszedł do głowy

Jerzy: To licz, jak ci napisałem. To najprostszy sposób.

salamandra:

1		1
	f2=a2−		e2 / * 4
4		4

f²=4a²−e² f=√4a²−e² i z tego?

Jerzy:

	1
Tak.Teraz: P(e) =		*f*e
	2

salamandra: f=√4a²−e²

	16−8e+e2
a2=
	16

	e2−8e+16
4a2=
	4

	−3e2−8e+16		−3e2−8e+16
f=√		−e2=√
	4		4

	1		−3e2−8e+16		1		√−3e2−8e+16
P=		*e*√		=		e*		=
	2		4		2		2

	e√−3e2−8e+16		√−3e4−8e3+16e2
=		=
	4		4

f(e)=−3e⁴−8e³+16e² wychdozi to samo

Jerzy:

	1
f(e) =		*√4a2 − e2*e = √4a2e2 − e4 i teraz licz pochodną.
	2

salamandra:

	−3+√33
to jest to samo, wychodzi nadal max dla
	3

Jerzy: Pochodna wyrażenia pod pierwiastkiem, to: −4e³ + 8a²e i teraz szukaj miejsc zerowych

salamandra: Tłumaczę Jerzy, że wychodzi to co u mnie policzyłem już z tego co podałeś

Jerzy: 15:39

	1		−4e3 + 8a2e
f'(e) =		*
	2		2√..........

Jerzy: 15:34 , co to jest na końcu f(e) = −3e⁴ − 8e³ + 16e²

salamandra: no rozpatruję tylko funkcję pod pierwiastkiem, wcześniej włączyłem "e" pod pierwiastek.

Jerzy: 15:48 , licz miejsca zerowe.

salamandra: Wyszły takie same jak w 14:54

Jerzy: −4e² + 8a² = 0, ile wynosi e ?

salamandra: Och, przepraszam, bo nie skopiowała mi się cała treść i pytają oczywiście dla jakiej długości

	−3+√33
przekątnej będzie max pole rombu. Wychodzi powtórzę po raz n−ty− max dla
	3

Jerzy: Odpowiedz na pytanie 16:26, bo funkcja f(e) osiąga maksimum dla takego e, które jest rozwiązaniem tego równania.

Jerzy: I nie powtarzaj głupot po raz n − ty.

salamandra: e²=2a² e=a√2

Jerzy: I to jest prawidłowe rozwiązanie.

salamandra: Nie przekonuje mnie to, nie widzę kompletnie Twoich przekształceń i dlaczego tak uparcie zostajesz przy "a", skoro je wyznaczyłem za pomocą "e".

Jerzy: a jest zadaną stałą,a e zmienną.

salamandra: Nic z tego nie rozumiem, mam dobrze czy nie,? Czemu mamy cokolwiek uzależniać od "a", skoro mamy "4" podane?

f123: @Jerzy pomyliles typy zadan.

Jerzy: Gdzie problem: a = 1 m , źle przeczytałem treść zadania.

ICSP: Tam była w ogóle treść gdzieś ? Bo nie widzę.

salamandra: Tak, dopisałem, że pytają dla jakiej długości przekątnej będzie max pole rombu

f123: @Jerzy tez sie na to nacialem na poczatku, ale chyba dlugosc przekatnej tez wliczamy do tego 4m?

salamandra: a≠1m

Jerzy: @salamandra, nie osłabiaj mnie,jeśli obwód rombu to 4 m, to jego bok = 1 m

Layla: @Jerzy skąd wiadomo, że obwód jest równy 4m?

salamandra:

Jerzy: Z treści zadania.

Layla: "Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną." Z treści zadania nie wynika przypadkiem, że na długość 4m składają się cztery ramiona rombu wraz z jego przekątną? Czyli L=4m− e

Jerzy: Zgoda,nie podał pełnej treści zadania.

salamandra: Podałem

Jerzy: Masz rację, 4a + e = 4 m

Jerzy: To ja źle zrozumiałem treść zadania.

Layla:

salamandra: W końcu doszliśmy do konsensusu