Wysokość ostrosłupa prawidłowego trójkątnego czarniecki: Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1. Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.

a7: https://matematykaszkolna.pl/forum/400880.html

Minato:

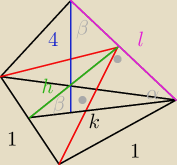
	√3
k =		(wysokość trójkąta równobocznego)
	2

	2
42+		k = l2
	3

	1		49		7
l2 =16 +		=		→ l =
	3		3		√3

4		h
	=
l		k

	√3		7
4*		=		h
	2		√3

	6
h =
	7

	1		6		3
P =		*1*		=
	2		7		7

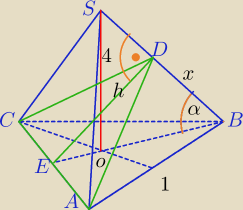Mila: Inny sposób:

	√3		√3
1)|EB|=		, |OB|=
	2		3

2) W ΔSOB:

	|OB|		√3		√3
ctgα=		⇔ctgα=		=
	H		3*4		12

	x		√3
W ΔEDB: ctgα=		⇔x=h*
	h		12

Z tw. Pitagorasa:

	√3		3
|EB|2=h2+x2⇔(		)2=h2+h2*
	2		144

3		49		3		48		36
	=		h2 ⇔h2=		*		=
4		48		4		49		49

	6
h=
	7

	3
PΔACD=
	7

===========

czarniecki: Tak mi wyszło jak wam, dzięki