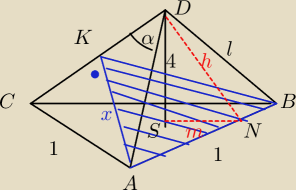
Wysokość ostrosłupa prawidłowego trójkątnego jest równa 4, a krawędź podstawy ma długość 1.
Ostrosłup przecięto płaszczyzną, która przechodzi przez krawędź podstawy oraz jest prostopadła
do przeciwległej krawędzi bocznej. Oblicz pole powierzchni tego przekroju.
| √3 | ||
1) m= | ||
| 6 |
| 3 | ||
42+ | =h2 | |
| 36 |
| 193 | ||
h2= | ||
| 12 |
| 1 | ||
h2+ | =l2 | |
| 4 |
| 196 | 49 | 7 | 7√3 | |||||
l2= | = | −> l= | = | |||||
| 12 | 3 | √3 | 3 |
| 98 | 7√3 | 7√3 | ||||
12= | −2* | * | *cosα | |||
| 3 | 3 | 3 |
| 98 | 147 | |||
1= | −2* | *cosα | ||
| 3 | 9 |
| −95 | −294 | ||
= | *cosα | ||
| 3 | 9 |
| 95 | ||
cosα= | ||
| 98 |
| √579 | ||
sinα= | ||
| 98 |
| l | x | ||
= | |||
| sin90 | sinα |
| 7√3 | √579 | ||
* | =x | ||
| 3 | 98 |
| √193 | ||
x= | ||
| 14 |
| 1 | 193 | ||
+hp2= | |||
| 4 | 196 |
| 144 | ||
hp2= | ||
| 196 |
| 6 | ||
hp= | ||
| 7 |
| 1 | 6 | 3 | ||||
P= | * | =U{6}[14}= | ||||
| 2 | 7 | 7 |
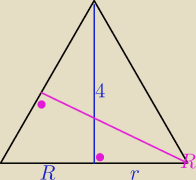R2 + 42 = x2
| √3 | |
2 + 42 = x2 | |
| 3 |
| √147 | ||
x = | ||
| 3 |
| 1 | √3 | 1 | √147 | ||||
* | * 4 = | * | * hplaszczyzny | ||||
| 2 | 2 | 2 | 3 |
| 6√441 | ||
hplaszczyzny = | ||
| 147 |
| 1 | 6√441 | 63 | 3 | |||||
P = | * | = | = | |||||
| 2 | 147 | 147 | 7 |