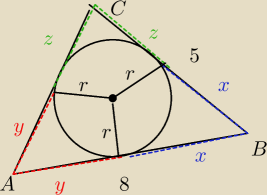
planimetria salamandra: Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy √3, a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta. Zaznaczyłem co mogłem i brakuje mi pomysłu

ABC: wiem ze masz zdrowie do rachunków i nie boisz się wielomianów, podnoś wzór Herona do kwadratu i przekształcaj

ABC: tu masz napisane co ci powinno wyjść ale jeśli jesteś ambitny nie zaglądaj dopóki sam nie zrobisz https://matematykaszkolna.pl/forum/401365.html

salamandra: hm, najpierw tak: y+x=8 y=8−x x+z=5 z=5−x y+z=AC=8−x+5−x=13−2x I to wstawiać teraz?

fil: pr = √p(p − a)(p − b)(p − c) i wyliczasz trzeci bok

salamandra:

	8+5+13−2x		26−2x
p (połowa obwodu)=		=		=13−x
	2		2

P=√(13−x−8)(13−x−5)(13−x−13+2x)=√(5−x)(8−x)x=√x²−13x+40)x=√x³−13x²+40x

	2P
r=
	a+b+c

	2√x3−13x2+40x		2√x3−13x2+40x
√3=		=
	13+13−2x		26−2x

ABC: p²r²=p(p−a)(p−b)(p−c) pr²=(p−a)(p−b)(p−c) trochę przekształceń i masz wielomian trzeciego stopnia

ABC: mówiłem ci żebyś do kwadratu podniósł najpierw

salamandra:

	2P
chciałem docelowo użyć r=		dlatego nie podnosiłem, a teraz się zastanawiam, czemu
	a+b+c

nie wychodzi

ABC: i niewiadomą ch...ą obrałeś , lepiej zajrzyj jednak do tamtego wątku jak to Eta oznaczyła

salamandra:

	√3
nie rozumiem skąd u Ety sinα=		się pojawia
	2

salamandra: Z Twojego pr²........ faktycznie wychodzi, ale pytanie dlaczego nie wychodzi z mojego?

fil: we wzorze na pole pod pierwiastkiem zabraklo ci (13 − x)

ABC: Eta trochę zgadła, to można uściślić pewnie ale nie chce mi się myśleć ale chodzi o to żebyś oznaczył boki 5,8,a i wtedy do Herona podstawiał

salamandra: Właśnie do tego doszedłem fil.... już drugie takie przeoczenie dzisiaj....

salamandra: rachunki masakryczne, ale wyszło: P=√13−x)(13−x−8)(13−x−5)(13−x−13+2x)=√(13−x)(5−x)(8−x)x=√(13x−x²)(40−8x−5x+x²)= =√(13x−x²)(x²−13x+40)=√13x³−x⁴−169x²+13x³+520x−40x²=√−x⁴+26x³−209x²+520x

	2P
r=
	a+b+c

	2*√−x4−26x3−209x2+520x
√3=		/2
	26−2x

	4*(−x4+26x3−209x2+520x)
3=
	676−104x+4x2

3(676−104x+4x²)=−4x⁴+104x³−836x²+2080x 2028−312x+12x²=−4x⁴+104x³−836x²+2080x −4x⁴+104x³−848x²+2392x−2028=0 −x⁴+26x³−212x²+598x−507=0 W(3)=0 dzielę wielomian przez (x−3).... zostaje: (−x³+23x²−143+169)(x−3)=0 −x³+23x²−143x+169=0 v x=3 W(13)=0 (−x²+10x−13)(x−13)(x−3)=0 −x²+10x−13=0 x1=5−2√3 x2=5+2√3 x3=13 x4=3 Tylko 3 pasuje, bo dla x=13 bok jest ujemny. Trzeci bok= 13−2x=13−6=7 Jeszcze pytanie− czy dla wyliczonego "x" powinienem sprawdzić, czy wyjściowy pierwiastek jest ≥ 0?

fil: wiesz, ze x ∊ (0, 5) i x ∊ Z

salamandra: Tak, ale nie trzeba sprawdzić czy przypadkiem dany x nie sprawia, że pierwiastek jest ujemny? Btw. Wejdź na discorda jak możesz

ABC: że tak powiem o k...a ! gdybyś oznaczył jak ci mówiłem rachunki byłyby łatwiejsze , na maturze ci czasu nie starczy przy twoich

salamandra: wybacz, upartość.... musiałem sobie udowodnić, że moim tez wyjdzie