Promień okręgu wpisanego w trójkąt o bokach czarniecki: Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy √3 , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta. Siedzę nad tym zadaniem już chyba z godzinę. Najpierw próbowałem to zrobić z tego, że absinγ/2=p*√3, ale tutaj doszedłem tylko do równania −c⁴+166c²−312c−3549, więc powodzenia w szukaniu miejsca zerowego tutaj. Następnie spróowałem to zrobić z tego, że p*√3=h*c, h wyznaczyyłem jako √3+x²+√3 (x to odcinek od wierzchołka c, do punktów gdzie promień pada na boki), c jako 13−2x, ale z tego wyszło mi równanie 4x⁴−52x³+208x²−156x+81... Już nie mam pomysłów

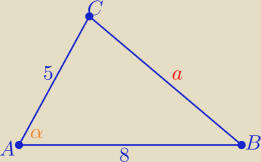
Eta: 2P=r(a+b+c) i 2P=8*5*sinα

	√3
40 sinα=√3(13+a) jeżeli sinα=		czyli α= 60o lub α=120o
	2

wtedy 20√3=√3(13+a) −− liczba całkowita 13+a= 20 ⇒ a=7

czarniecki:

	√3
Skąd to, że sin alfa=
	2

ABC: przy oznaczeniach Ety, jak się podniesie wzór Herona do kwadratu i trochę poprzekształca, dochodzimy do równania : a³−13a²+3a+273=0 sprawdzając dzielniki 273 mamy pierwiastek 7 i rozkład (a−7)(a²−6a−39)=0 z drugiego nawiasu jeden pierwiastek ujemny a drugi dodatni ale nie jest liczbą całkowitą

czarniecki: Tak samo wychodzi w moim wielomianie, ale chyba powinno być jakieś inne rozwiązanie?

ABC: wypisywałeś wielomiany czwartego stopnia to ci napisałem rozwiązanie z wielomianem niższego , zapewne są inne rozwiązania ale to nie przekracza poziomu rozszerzonego liceum − twierdzenia o pierwiastkach całkowitych jeszcze nie wyrzucili z programu

Mila: Możesz liczyć na piechotę i sprawdzać, czy przy dobranym trzecim boku zgadza się długość r. a∊{4,5,6,7,8,9,10,11,12} po drodze wymyślisz, które długości pominąć.

Eta: