pochodne
anonim123: f(x)=−x3+3x2−1 Jak wskazać kiedy funkcja maleje a kiedy rośnie mi wychodzi po obliczeniu
pochodnej
x(x−2) ≤ 0 i porównaniu do zera
14 maj 16:45
14 maj 16:57
a7:
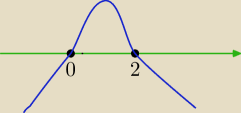
przepraszam odwrotnie
14 maj 16:58
a7:
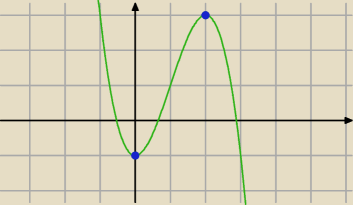
14 maj 16:59
14 maj 17:01
anonim123: czyli rosnąca jest pochodna od zera do dwóch przedział zamknięty?
14 maj 17:29
anonim123: bo mi wychodzi coś innego −3x(x−2) ≥ 0/:−3 x(x−2) ≤0 czy to jest źle?
14 maj 17:48
a7: funkcja jest rosnąca , gdy jej pochodna jest większa od zera (przedział otwarty),
miejsca zerowe pochodnej Ci wyszły te same x=0 i x=2
funkcja jest rosnąca dla x∊(0,2)
14 maj 17:52
a7: nie robimy w ten sposób, o ile mi wiadomo tylko przyrównujemy do zera pochodną taką jaka
wychodzi a potem patrzymy jak ta pochodna zmienia znak
14 maj 17:58
anonim123: Ale znak nierówności mam inny i wychodzą różne rozwiązania od twoich.
Dlaczego przedział otwarty a nie zamknięty?

14 maj 17:59
anonim123: Możesz wyjaśnić

14 maj 18:03
a7: funkcja jest rosnąca , gdy f'(x)>0
robimy tak, że liczymy pochodną
wychodzi f'(x)=−3x2+6x=−3x(x−2)
teraz przyrównujemy ją do zera, (a NIE robimy nierówność)
−3x(x−2)=0 x=0 lub x=2
teraz rysujemy na osi miejsca zerowe pochodnej i sprawdzamy jak zmienia znak
dla x∊(0,2) pochodna jest dodatnia (większa od zera), więc w tym przedziale funkcja jest
rosnąca
14 maj 18:04
a7: natomiast Twoim sposobem wyjdzie de facto to samo
14 maj 18:05
a7:
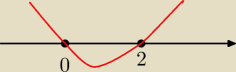
3x(x−2)<0
dla x∊(0,2) funkcja jest rosnąca
ale tak chyba nie robimy, bo by się wszystkim myliło
14 maj 18:07
a7: może się jeszcze wypowie jakiś większy autorytet
14 maj 18:07
anonim123: A to nie powinno być w przedziale domkniętym [0,2]?
14 maj 18:09
14 maj 18:16
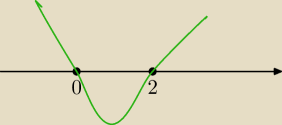 http://matematykadlastudenta.pl/strona/198.html
f'(x)=−3x2+6x=3x(−x+2)
przyrównujemy pochodną do zera x=0 lub x=2
funkcja rosnąca dla x∊(−∞,0)U(2, ∞) malejąca dla x∊(0,2)
http://matematykadlastudenta.pl/strona/198.html
f'(x)=−3x2+6x=3x(−x+2)
przyrównujemy pochodną do zera x=0 lub x=2
funkcja rosnąca dla x∊(−∞,0)U(2, ∞) malejąca dla x∊(0,2)
 przepraszam odwrotnie
przepraszam odwrotnie



 3x(x−2)<0
dla x∊(0,2) funkcja jest rosnąca
ale tak chyba nie robimy, bo by się wszystkim myliło
3x(x−2)<0
dla x∊(0,2) funkcja jest rosnąca
ale tak chyba nie robimy, bo by się wszystkim myliło