wyjasnienie
f123: W parabolę o równaniu y=−x2+10x wpisano prostokąt w taki sposób, że dwa wierzchołki
tego prostokąta o obu współrzędnych dodatnich leżą na wykresie paraboli, a dwa pozostałe
wierzchołki leżą na osi OX . Wyznacz największe możliwe pole takiego prost.
Wyjasnilby ktos klarownie, dlaczego dlugosc podstawy boku prostokata lezacego na osi x to 2x −
10 a nie 10 − 2x

4 maj 22:12
ICSP: czym jest x?
4 maj 22:36
ICSP: trochę niefortunna nazwa (parabola też jest od niego zależna)
4 maj 22:38
f123: x − pierwsza wspolrzedna pierwszego punktu (idac od lewej) czyli przykladowo xa mozna nazwac
4 maj 22:40
f123:
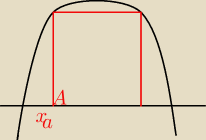
4 maj 22:41
ICSP: 10 − 2a
4 maj 22:41
4 maj 22:44
ICSP: Eta powiedziała, ze odwrotnie napisała.
Widać, że a musi być mniejsze od 5.
Podstaw tą wartość do 2a − 10 oraz 10 − 2a i zobacz któa jest ujemna a która dodatnia.
Potem do obliczeń bierzesz tę dodatnią.
4 maj 22:48
Mila:
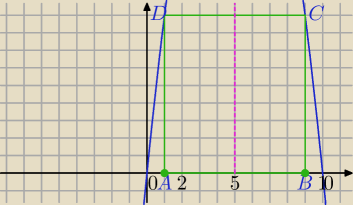
f(x)=−x
2+10x
A=(a,0), B=(10−a,0), a∊(0,5)
|AB|=
√(10−a−a)2)=
√(10−2a)2=|10−2a|=10−2a dla a<5
10−2a>0⇔10>2a⇔a<5
4 maj 22:57
f123: aaa chyba rozumiem juz, liczymy w zaleznosci od 'a'
jesli a < 5
|AB| = 10 − 2a
w przeciwnym razie
|AB| = 2a − 10
4 maj 22:59


 f(x)=−x2+10x
f(x)=−x2+10x