Jak to uzasadnić? Study1352: W trapezie równoramiennym ABCD poprowadzono przekątne, które przecięły się w punkcie S. Uzasadnij, że trójkąty ASD i BSC są przystające.

a7: ja bym uzasadniła, że są przystające z cechy kąt, kąt, kąt, ale chyba równie dobrze można z cechy kąt bok kąt https://matematykaszkolna.pl/strona/513.html

Bogdan: Cecha kąt, kąt, kąt jest cechą podobieństwa, a nie przystawania trójkątów.

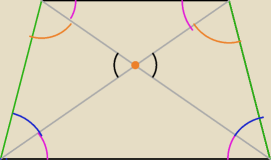
a7: różowe kąty są sobie równe (przy każdej z jednej przekątnych są naprzemianległe, a równe sobie gdyż trójkąty ABD i ABC są przystające (b,k,b)) więc i niebieskie są sobie równe i pomarańczowe, a także czarne to kąty wierzchołkowe , zielony bok jest równy drugiemu, gdyż jest to trapez równoramienny także można uzasadniać i z cechy kkk i kbk

a7: o faktycznie, przepraszam, w takim razie kbk

a7: @Study czy taka podpowiedż/wskazówka jest wystarczająca czy przeprowadzić uzasadnienie jak do szkoły

study1352: okey dziękuuję

study1352: wystarczy