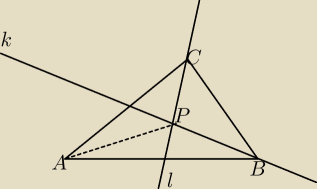
W trójkącie ABC dany jest wierzchołek A(2,−5) oraz równania prostych zawierający Pawo: W trójkącie ABC dany jest wierzchołek A(2,−5) oraz równania prostych zawierających jego środkowe k: 4x+5y=0 i l: x−3y=0. Wyznacz wierzchołki B i C. Zacząłem to robić tak: Policzyłem, że A nie należy do żadnej z tych prostych Punkt przecięcia prostych k i l wyszedł mi P=(0,0), więc |AP|=√29 Oznaczyłem, że B(x_B, −4/5x_B), C(x_C, 1/3x_C) I teraz z własności środkowych, że |AP|=|BP=|CP|=√29, chciałem policzyć wierzchołki B i C ale mi nie wychodzi. Wiem, że można robić to zadanie z wektorów i pewnie szybko wychodzi, ale średnio za nimi przepadam. Co robię nie tak?

a7: https://matematykaszkolna.pl/strona/495.html

a7: https://matematykaszkolna.pl/forum/316765.html

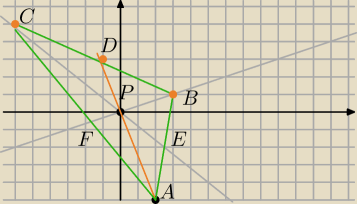a7: wyznaczamy D prosta AP ma równanie y=−5/2*x PD=√29/2 D=(x_D;−5/2x_D) x_d²+(−5/2)x_d²=29/4 x_D=1 lub x_D=−1 y_D=5/2 D=(−1, 5/2)

	xC+xB
|CD|=|DB| oraz		=−1 xc=−2−xb yC=5−yB
	2

teraz można porównać długości CD i DB po czym podstawić x_C=−2−x_B i wyjdzie , ale to dużo liczenia

a7: wychodzi x_B=3 y_B=1 x_C=−5 y_C=4