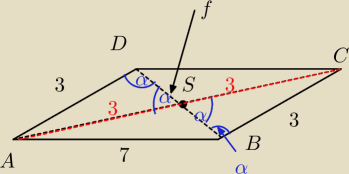
planimetria salamandra: W równoległoboku boki mają długości 3 i 7, a jedna z przekątnych ma długość 6. Oblicz cosinus kąta ostrego pod jakim przecinają się przekątne tego równoległoboku. ze wzoru 2a²+2b²=e²+f² Eta Te kąty α zaznaczyłem tam również jeden wierzchołkowy i dwa wynikające z tego, że powstają trójkąty równoramienne, jako że w równoległoboku przekątne przecinają się w połowie. a=7 b=3 2*49+2*9=36+f² 116−36=f² f²=80 −> f=4√5 z tw. cosinusów w ΔASD 9=9+20−12√5*cosα −20=−12√5*cosα

20
	=cosα
12√5

	5√5		√5
U{5}{3√5=cosα=		=
	15		3

Jest ok?

wredulus_pospolitus: Pragnę tylko zwrócić uwagę na to, że .... ta przekątna NIE MOŻE mieć długości 6 (jest ona krótsza od boku |AB| = 7 )

salamandra: a DB?

wredulus_pospolitus: już prędzej

salamandra: jak to rozróżnić, bo nie bardzo widzę

a7: https://matematykaszkolna.pl/forum/400564.html

salamandra: jak wy wyszukujecie tych zadań, mi nigdy nic nie wyskakuje jak wpiszę treść

salamandra: @wredulus, już wyjaśnione na discordzie jak coś a propos tej przekątnej

salamandra: szczęśliwie nie wpływa to tutaj na rozwiązanie

a7: akurat pamiętałam, że było wczoraj i szukałam "na liście"