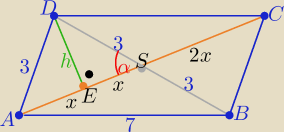
 e=6, f= 4x, x>0
ΔADS równoramienny to..................⇒ oznaczenia na rys.
W każdym równoległoboku zachodzi równość
f2+e2=2(a2+b2)
16x2+36=2*58 ⇒ x=√5
to cosα= √5/3
============
e=6, f= 4x, x>0
ΔADS równoramienny to..................⇒ oznaczenia na rys.
W każdym równoległoboku zachodzi równość
f2+e2=2(a2+b2)
16x2+36=2*58 ⇒ x=√5
to cosα= √5/3
============
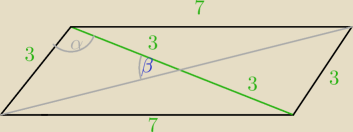 z tw. cosinusów
72=32+62−2*3*6*cosα cosα=−1/9 cosβ= (cos(90−α/2)=sin(α/2)
sinα=√1−1/81=4√5/9 sinα=2sin(α/2)cos(α/2)
sin(α/2)=sinα/(2cos(α/2))
cosα=cos2(α/2)−1 cos(α/2)=2/3
cosβ= sin(α/2)=√5/3
?
z tw. cosinusów
72=32+62−2*3*6*cosα cosα=−1/9 cosβ= (cos(90−α/2)=sin(α/2)
sinα=√1−1/81=4√5/9 sinα=2sin(α/2)cos(α/2)
sin(α/2)=sinα/(2cos(α/2))
cosα=cos2(α/2)−1 cos(α/2)=2/3
cosβ= sin(α/2)=√5/3
?
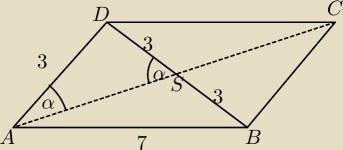 Obliczamy cos kąta ADS z tw. cosinusów
|AB|2 = |AD|2 + |DB|2 − 2*|AD|*|DB|*cos|∡ADB|
72 = 32 + 62 − 2*3*6*cos|∡ADB|
Obliczamy cos kąta ADS z tw. cosinusów
|AB|2 = |AD|2 + |DB|2 − 2*|AD|*|DB|*cos|∡ADB|
72 = 32 + 62 − 2*3*6*cos|∡ADB|
| 32+62−72 | ||
cos|∡ADB| = | ||
| 36 |
| 1 | ||
cos|∡ADB| = − | ||
| 9 |
| a+b+c | ||
p = | = 8 | |
| 2 |
| 1 | ||
PASD = | *3*3*sin(180o−2α) | |
| 2 |
| 9 | ||
2√5 = | *sin(2α) | |
| 2 |
| 4√5 | ||
sin(2α) = | ||
| 9 |
| 4√5 | ||
2sinα*cosα = | ||
| 9 |
| 2√5 | ||
{sinα*cosα = | ||
| 9 |
| 2√5 | ||
{sinα = | ||
| 9cosα |
| 2√5 | ||
( | )2 + cos2α = 1 | |
| 9cosα |
| 20 | |
+ cos2α = 1 | |
| 81cos2α |
| 20 | |
+ x = 1 |*x | |
| 81x |
| 20 | |
+ x2 = x | |
| 81 |
| 20 | ||
x2 − x + | = 0 | |
| 81 |
| 4 | 5 | |||
x = | ∨ x = | |||
| 9 | 9 |
| 2 | 2 | √5 | √5 | |||||
cosα = | ∨ cosα = − | ∨ cosα = | ∨ cosα = − | |||||
| 3 | 3 | 3 | 3 |
| 2 | ||
cosα = | = 0,66666... → α ≈ 48o (odrzucamy) | |
| 3 |
| √5 | ||
cosα = | ≈ 0,745 → α ≈ 42o (spełnia założenie α<45o) | |
| 3 |
| √5 | ||
Odp. cosα = | ||
| 3 |


 I tak właśnie ford .... pojechałeś
I tak właśnie ford .... pojechałeś 

