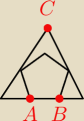
kąt Juliusz: Pieciokąt foremny jest wpisany w trójkat równoboczny (rys). Oblicz miarę kąta ACB

an: Czy to Ty rozwiązujesz równania różniczkowe np https://matematykaszkolna.pl/forum/391578.html pytam tak ciekawości.

Juliusz: Nie to nie ja nie wiedziałem, pewnie ma tak samo na imię

a7: czy wystarczy sin α?

a7: i orientacyjna wartość α odczytana z tablic?

Juliusz: Tak wystarczy

Juliusz: Sam sinus

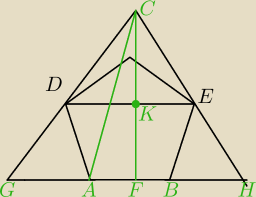
a7: AB=b GH=a

	√5+1
DE=d=		*b
	2

z podobieństwa trójkątów CKE i CFE wynika, że a=2b

	√3
AF=1/2*b CF=b√3 to sinα/2=U{√13{13} cos(α/2)=2*
	13

to sinα=2sin(α/2)cos(α/2)=4U{√3{13}≈0,5329387 to α≈32^o

a7: widzę, że dużo chochlików, czy coś wyjaśnić?

a7: oj chyba źle, sprawdzam

Mariusz: CKE i CFE są podobne ? Wg mnie kąty się nie zgadzają CKE i CFH są podobne (z równości kątów) P.S. Byłeś jednym z nielicznych którzy napisali opinię o pewnym moderatorze

a7: ja? ja żadnej opinii o moderatorach nie pisałam to an

Mila: To chyba nie do Ciebie a7 , nie bardzo wiem o co chodzi, nie śledziłam sytuacji "kryzysowej " na forum. Pewnie były pretensje. Na zadanie spojrzę później.

a7: sinα≈0,392 więc α≈23^o ?

a7: Dzień dobry Milu, sytuacja "kryzysowa" się rozpętała przy wątku o wirusie, ale teraz chyba wszyscy jesteśmy drażliwi, wydaje mi się, że bywały tu raczej gorsze scysje, ale nie mam zdania

Mila: a7 Dzień dobry, miło Cię tu widzieć Ja zalecam święty spokój

a7: no zaglądam prawie codziennie, ale nie zawsze znajduję "coś dla siebie"

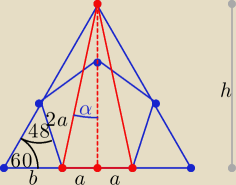
Bogdan: sin48^o ≈ 0,743145, √3 ≈ 1,732051

	2a		b		4a*sin48o
Z twierdzenia sinusów:		=		⇒ b =
	sin60o		sin48o		√3

	4a*sin48o
h = (a + b)*√3 = (a +		) * √3 = a(√3 + 4sin48o)
	√3

	a		a		1
tgα =		=		=		⇒ α = 12o i 2α = 24o
	h		a(√3 + 4sin48o)		√3 + 4sin48o

(wartości sin48^o i tg12^o odczytane z tablic)