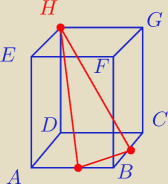
 Prostopadłościan ABCDEFGH, którego podstawą jest kwadrat o boku 4, a wysokość ma długość
6, przecięto płaszczyzną przechodzącą przez środki krawędzi AB i BC oraz wierzchołek H. Oblicz
pole otrzymanego przekroju.
Wiem, że tutaj jest rozwiązanie: https://matematykaszkolna.pl/forum/372680.html
Moje pytanie jest następujące: Skąd miałbym wiedzieć, że przekrojem w tym zadaniu jest
pięciokąt?
Patrzyłem na link wrzucony przez Mile −>
https://math-comp-educ.pl/przekroje-szescianu/
Na animacjach widać dlaczego przekrój jest pięciokątem, ale z czego to wynika? Muszę się
nauczyć na pamięć tych animacji, żeby wiedzieć, że przekrój w tym zadaniu nie jest
trójkątem takim jak narysowałem tylko pięciokątem? Jeśli trzeba tu polegać tylko na wyobraźni
to przecież nie jest to oczywiste, że przekrój w tym przypadku jest pięciokątem.
Prostopadłościan ABCDEFGH, którego podstawą jest kwadrat o boku 4, a wysokość ma długość
6, przecięto płaszczyzną przechodzącą przez środki krawędzi AB i BC oraz wierzchołek H. Oblicz
pole otrzymanego przekroju.
Wiem, że tutaj jest rozwiązanie: https://matematykaszkolna.pl/forum/372680.html
Moje pytanie jest następujące: Skąd miałbym wiedzieć, że przekrojem w tym zadaniu jest
pięciokąt?
Patrzyłem na link wrzucony przez Mile −>
https://math-comp-educ.pl/przekroje-szescianu/
Na animacjach widać dlaczego przekrój jest pięciokątem, ale z czego to wynika? Muszę się
nauczyć na pamięć tych animacji, żeby wiedzieć, że przekrój w tym zadaniu nie jest
trójkątem takim jak narysowałem tylko pięciokątem? Jeśli trzeba tu polegać tylko na wyobraźni
to przecież nie jest to oczywiste, że przekrój w tym przypadku jest pięciokątem. 
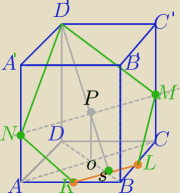 1) Odcinek KL , odcinek SD'
2) Przekątne podstawy
3) OP⊥AC
4) Odcinek MN || AC i przechodzący przez punkt P, potem LM i KN
5) Odcinek MD' i ND'
================
1) Odcinek KL , odcinek SD'
2) Przekątne podstawy
3) OP⊥AC
4) Odcinek MN || AC i przechodzący przez punkt P, potem LM i KN
5) Odcinek MD' i ND'
================
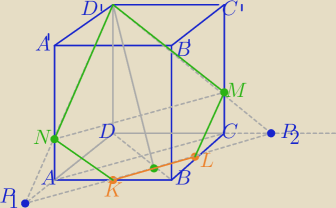 II sposób
1) odcinek KL
2) Przekątne podstawy , Przedłużenie DC i DA,
3) Przedłużenie KL− otrzymujesz P1 i P2
4) Przerywaną linią odcinek P1D', Odcinek P2D'− otrzymujesz punkty : M i N
5) Odcinki : LM, MD' ; KN, ND'
========================
II sposób
1) odcinek KL
2) Przekątne podstawy , Przedłużenie DC i DA,
3) Przedłużenie KL− otrzymujesz P1 i P2
4) Przerywaną linią odcinek P1D', Odcinek P2D'− otrzymujesz punkty : M i N
5) Odcinki : LM, MD' ; KN, ND'
========================
 Rozwiązanie (korzystam z rysunku 18:34):
Po przecięciu prostopadłościanu płaszczyzną otrzymujemy pięciokąt składający się z trójkąta
równoramiennego MND' oraz z trapezu równoramiennego MNKL. Pole pięciokąta będzie sumą pól
trójkąta MND' i trapezu MNKL.
1) Wyznaczenie podstaw obu figur:
Z tw. Pitagorasa dla trójkąta KLB:
|KL|2 = 8
|KL| = 2√2
|AC| = |DB| = 4√2
|MN| || |AC| ⋀ |MN| = |AC| ⇒ |MN| = 4√2
2) Wyznaczenie wysokości obu figur do policzenia ich pól:
1. △D'DS ~ △POS na podst. cechy KKK (*)
2. ΔACB ~ ΔKLB w skali k = 2 ⇒ |BS| to wysokość ΔKLB, ponieważ |BO| to wysokość
ΔACB
Z tw. Pitagorasa dla ΔKSB:
|BS|2 + (√2)2 = 22
|BS|2 = 2
|BS| = √2
|DS| = 4√2 − √2 = 3√2
Z tw. Pitagorasa dla ΔD'DS:
62 + (3√2)2 = |D'S|2
|D'S|2 = 54
|D'S| = √54 = 3√6
|OS| = 2√2 − √2 = √2
(*) Z podobieństwa trójkątów ΔD'DS i ΔPOS:
Rozwiązanie (korzystam z rysunku 18:34):
Po przecięciu prostopadłościanu płaszczyzną otrzymujemy pięciokąt składający się z trójkąta
równoramiennego MND' oraz z trapezu równoramiennego MNKL. Pole pięciokąta będzie sumą pól
trójkąta MND' i trapezu MNKL.
1) Wyznaczenie podstaw obu figur:
Z tw. Pitagorasa dla trójkąta KLB:
|KL|2 = 8
|KL| = 2√2
|AC| = |DB| = 4√2
|MN| || |AC| ⋀ |MN| = |AC| ⇒ |MN| = 4√2
2) Wyznaczenie wysokości obu figur do policzenia ich pól:
1. △D'DS ~ △POS na podst. cechy KKK (*)
2. ΔACB ~ ΔKLB w skali k = 2 ⇒ |BS| to wysokość ΔKLB, ponieważ |BO| to wysokość
ΔACB
Z tw. Pitagorasa dla ΔKSB:
|BS|2 + (√2)2 = 22
|BS|2 = 2
|BS| = √2
|DS| = 4√2 − √2 = 3√2
Z tw. Pitagorasa dla ΔD'DS:
62 + (3√2)2 = |D'S|2
|D'S|2 = 54
|D'S| = √54 = 3√6
|OS| = 2√2 − √2 = √2
(*) Z podobieństwa trójkątów ΔD'DS i ΔPOS:
| |DS| | |OS| | ||
= | |||
| |D'S| | |PS| |
| 3√2 | √2 | ||
= | |||
| 3√6 | |PS| |
| 1 | 2√2 + 4√2 | |||
PKLMNH = | * 4√2 * 2√6 + | * √6 = 4√12 + 3√12 = 7√12 = | ||
| 2 | 2 |

 Można trochę krócej, może przed maturą wrócimy do tego, zapisz to sobie gdzieś
Można trochę krócej, może przed maturą wrócimy do tego, zapisz to sobie gdzieś
