trójkąt anka : W trójkąt ABC wpisano okrąg o promieniu R. Równolegle do boków trójkąta poprowadzono styczne do okręgu,które odcięły przy wierzchołkach A,B,C trzy mniejsze trójkąty zawarte w trójkącie ABC. W tak otrzymane trójkąty wpisano okręgi o promieniach r1,r2,r3 Wykaż,że r1+r2+r3=R

maks: https://matematykaszkolna.pl/forum/135682.html

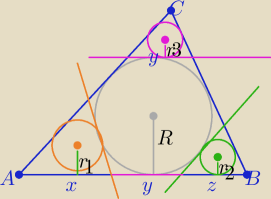
Eta: Z podobieństwa małych trójkątów do ΔABC w skalach:

x

r1

y

r2

z

r3

k1=

=

, k2=

=

, k3=

=

x+y+z

R

x+y+z

r

x+y+z

R

	x+y+z
k1+k2+k3=		=1
	x+y+z

to

	r1		r2		r3
		+		+		=1 /*R
	R		R		r

r₁+r₂+r₃=R ============ c.n.w.

Eta: Poprawiam chochliki W mianowniku trzeciego ułamka oczywiście ma być R i w mianowniku k₂ też R

maks: Zerkniesz na to: https://matematykaszkolna.pl/forum/400063.html