1. W trójkąt ABC wpisano okrąg o
promieniu r. Styczne do tego okregu odcinaja trzy trojkaty (styczne są równoległe do boków), w
które wpisano okręgi o promieniach r1,r2,r3. Udowodnij, że r=r1+r2+r3
2. Znajdź długość dwusiecznej kąta prostego w trójkącie prostokątnym o przyprostokątnych a,b.
3. Dwa okręgi o promieniach r1=3 i r2=9 są styczne zewnetrznie. Oblicz pole oraz obwód figury
ograniczonej tymi okręgami i ich wspólną styczną zewnętrzną.
Bardzo proszę o pomoc 
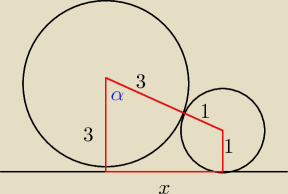3)
najpierw oblicz pole czerwonego trapeza (nie jest trudne).
Następnie wyznacz α, aby wiedzieć jakie wycinka obu okręgów 'odjąć' od otrzymanego pola.
I masz wynik
tylko jak wyznaczyć alfę? Czy to będzie
60?
| 3−1 | ||
a wyznaczasz z cos α = | ... różnice podstaw trapezu przez ramię trapezu | |
| 3+1 |
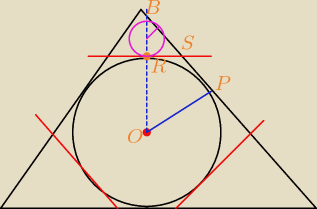wskazówka do pierwszego zadania:
zauważ, że okrąg (ten duży) leży na przecięciu się wysokości ... czyli środki małych okręgów
także będą leżeć na tychże wysokościach (tylko każdy na jednej z nich) ... wynika to z
założenia o stycznych równoległych do boków trójkąta.
Zauważ podobieństwa trójkątów prostokątnych tworzonych przez wysokość dużego trójkąta i promień
dużego (oraz każdego małego) okręgu.
Powinieneś z tego dać radę ułożyć takie proporcje, że Ci wyjdzie.
Niestety rysunek mało estetyczny 
i raczej niewiele z niego widać