Współliniowość punktów w ostrosłupie - matura czerwiec 2014
Shizzer: Podstawą ostrosłupa jest kwadrat ABCD o boku długości 25. Ściany boczne ABS i BCS
mają takie same pola, każde równe 250. Ściany boczne ADS i CDS też mają jednakowe pola, każde
równe 187,5. Krawędzie boczne AS i CS mają równe długości. Oblicz objętość tego ostrosłupa.
Byłbym wdzięczny za wytłumaczenie mi dlaczego w tym
https://matematykaszkolna.pl/forum/255466.html
rozwiązaniu punkty K i L są
współliniowe ze spodkiem wysokości? Muszę sobie to jakoś wyobrazić
przestrzennie czy jest na to jakaś reguła?
17 kwi 22:23
Shizzer: Oo już chyba wiem. Czy to wynika z rzutów prostokątnych wysokości przeciwległych ścian bocznych
na płaszczyznę podstawy?
17 kwi 22:36
f123: 
17 kwi 22:44
f123: zastanowiles sie dwa razy zanim zadales to pytanie


17 kwi 22:48
Shizzer: Dziś już długo robiłem zadania, a to jedno nie daje mi spokoju. Chciałbym się po prostu
dowiedzieć
skąd wynika współliniowość tych punktów. Nie wiem czy poprawne pytanie zadałem, ale naprawdę
już jestem dziś zmęczony

17 kwi 22:50
f123:
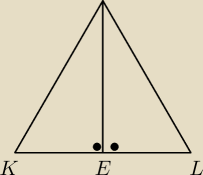
"wyciagasz" trojkat z wysokoscia ostroslupa. Bogdan narysowal tam ten trojkat. to K, E, L sa
wspoliniowe
17 kwi 23:11
Shizzer: Chyba się nie zrozumieliśmy − ja doskonale widzę tam ten trójkąt.
Chodziło mi jedynie o to dlaczego punkt E jest współliniowy z K i L. Konkretniej: Mamy punkty
padania
wysokości oznaczone jako K i L. Następnie łączymy je prostą natomiast nie mogłem zrozumieć
dlaczego ta prosta przecina spodek wysokości ostrosłupa? Czy nie mogłoby być tak w jakimś
przykładowym ostrosłupie o innych parametrach, że prosta łącząca punkty na które upadają
wysokości
NIE przecięłaby spodka wysokości?
17 kwi 23:19
Mila:
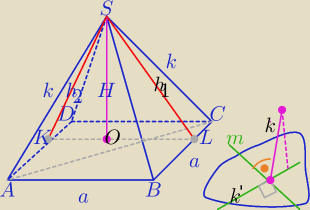
a=25
|AC|=25
√2
Ostrosłup jest "przechylony " w kierunku ściany SDC
O − rzut prostokątny punktu S na płaszczyznę
Tw. o trzech prostopadłych:
Prosta m jest prostopadła do prostej k, wtedy i tylko wtedy,
gdy jest prostopadła do prostej k'.
Narysowano wysokość h
1, h
1⊥BC − to jest oczywiste ,
OL jest rzutem prostokątnym h
1 na płaszczyznę ABCD
Dalej mamy: KL⊥BC i KL⊥AD,
LO jest rzutem prostokątnym h
1 na płaszczyznę ABCD
OK jest rzutem KS na płaszczyznę ABCD
⇔KS⊥KL
17 kwi 23:48
Shizzer: Na ten moment ciężko mi przychodzi zrozumienie tego zagadnienia.

Jak powinny wyglądać moje
kroki w "konstruowaniu" takiego ostrosłupa? Czy tak?
1. Wyznaczam spodek wysokości ostrosłupa i szkicuję jego wysokość
2. Szkicuję wysokość h1, która pada obojętnie w jakim punkcie na ramię BC.
3. Rzut prostokątny h1 ma płaszczyznę podstawy
I teraz właśnie w mojej głowie pojawia się pytanie "W jakim dokładnie punkcie wysokość h2
powinna
upadać?". Tego nie potrafię jeszcze wykonać. Rozumiem, że jestem w stanie ten punkt padania h2
wyznaczyć posługując się twierdzeniem o trzech prostych prostopadłych?
Wiem
Milu, że próbowałaś mi to wyjaśnić, ale na ten moment jeszcze nie umiem tego sposobu
myślenia przyswoić. Jeśli moje kroki są dobre to jutro spróbuję to przemyśleć jeszcze raz

18 kwi 00:17
Mila:
1) Szkicujesz Ostrosłup i wiesz, że spodek wysokości
nie znajduje się na przecięciu przekątnych podstawy
2) Szkicujesz h
1 i jej rzut na ABCD, masz pkt O
3) prowadzisz prostą przez ten rzut
− masz punkt K
4) Rysujesz h
2
Poprawiasz rysunek i rozwiązujesz.
Do jutra, może wymyślę ćwiczenie , abyś lepiej zrozumiał.
Dobranoc

18 kwi 00:28
Shizzer:
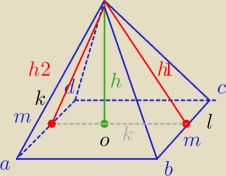
Dzień dobry

Zregenerowałem mózg i chyba na coś wpadłem. Oto jak rozumiem współliniowość punktów L, O i K
(przepraszam za oznaczenia małymi literami, ale nie wiem jak napisać wielkie).
1. Szkic ostrosłupa − nie jest to ostrosłup prawidłowy zatem jego spodek wysokości nie znajdzie
się
w punkcie przecięcia się przekątnych podstawy.
2. Szkicuję h1 i jej rzut prostokątny na płaszczyznę ABCD, dzięki temu otrzymuję punkt O.
3. W tym momencie mamy sytuację, w której mogę skorzystać z
twierdzenia o trzech prostych prostopadłych. Zatem na moim rysunku mamy: m ⊥ h1 ⇔ m ⊥ k.
4. Po drugiej stronie wysokości ostrosłupa mamy taką samą sytuację. Skoro ABCD to kwadrat
zatem znów pojawia się prosta m. Więc: m ⊥ h2 ⇔ m ⊥ k.
Z kroków 3 i 4 wynika, że punkty K, O, L są współliniowe. Czy tak to powinienem rozumieć?
18 kwi 12:07
Shizzer: Poprawka w punkcie 4 −> tam nie pojawia się oczywiście taka sama prosta m tylko prosta
równoległa
do prostej m znajdującej się po drugiej stronie kwadratu ABCD.
18 kwi 12:13
Bogdan:
Wielkie litery jak zwykle zapisujemy z wciśniętym klawiszem Shift
18 kwi 16:02
Shizzer: Szczerze mówiąc zawsze pisałem je z przyciskiem Caps Lock naciśniętym

Będę wiedział na przyszłość
18 kwi 16:31
Mila:
Shizzer , dzień dobry.

Najprościej tutaj to będzie, jeśli przetniesz ostrosłup płaszczyzną prostopadłą do
ABCD wyznaczoną przez punkty: S, O i taką, aby krawędź przecięcia była równoległa do AB.
18 kwi 18:36
Shizzer: Tą płaszczyzną jest trójkąt KLS. Tylko gdybym przeciął ostrosłup taką
płaszczyzną znów zastanawiałbym się czy ramiona tej płaszczyzny na
pewno są prostopadłe do krawędzi podstawy ostrosłupa. Dzięki
twierdzeniu o trzech prostych prostopadłych już wiem, że są co daje
mi w rezultacie zrozumienie dlaczego K, O i L są współliniowe

18 kwi 18:47
Shizzer: Ale rzeczywiście jeśli pomyślę o trójkącie KLS jako o płaszczyźnie tnącej ostrosłup
jest łatwiej zatem dziękuję

18 kwi 18:48
Mila:
K,O,L −współliniowe, to znasz długość odcinka KL.
18 kwi 19:26
Shizzer:
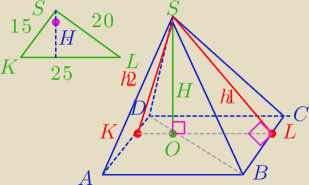
Tak wynosi ona 25. Rozwiązałem już to zadanie dziś rano. Wrzucę to może ktoś skorzysta:
Punkty K, O, L są współliniowe co wynika z twierdzenia o trzech prostych prostopadłych:
|BC| ⊥ |OL| ⇔ |BC| ⊥ |SL| zatem |BC| ⊥ |OL| i |BC| ⊥ |SL|
Skoro |AD| || |BC| to taka sama sytuacja dzieje się na ścianie ADS.
P△BCS = P△ABS = 250
P△ADS = P△DCS = 187,5
| ⎧ | 12 * 25 * h1 = 250 | |
| ⎩ | 12 * 25 * h2 = 187,5 |
|
△KLS jest trójkątem pitagorejskim powiększonym o skalę k = 5 ⇒ |∡KSL| = 90
o
Wewnątrz tego trójkąta prostokątnego mamy wysokość ostrosłupa, którą oznaczyłem jako H.
| ⎧ | x2 + H2 = 152 | |
| ⎩ | (25 − x)2 + H2 = 202 |
|
| ⎧ | H2 = 152 − x2 | |
| ⎩ | (25 − x)2 + (152 − x2) = 202 |
|
Rozwiązując ten układ równań otrzymujemy x = 9.
Podstawiając obliczony x do układu równań obliczymy H potrzebne do obliczenia V.
H = 12
V =
13 * 25
2 * 12 =
6253 * 12 = 2500
18 kwi 20:11
Mila:
H− można obliczyć tak:
ΔKLS− Δprostokątny o bokach 15,20, 25 ( co zauważyłeś i nie wykorzystałeś)
| | 1 | | 1 | |
PΔKLS= |
| *|KL|*H⇔ |
| *25*H=150 |
| | 2 | | 2 | |
H=12
18 kwi 20:37
Shizzer: Umknęło mi to, a byłoby dużo szybciej. Dziękuję raz jeszcze!
18 kwi 20:56
Mila:

18 kwi 21:08




 "wyciagasz" trojkat z wysokoscia ostroslupa. Bogdan narysowal tam ten trojkat. to K, E, L sa
wspoliniowe
"wyciagasz" trojkat z wysokoscia ostroslupa. Bogdan narysowal tam ten trojkat. to K, E, L sa
wspoliniowe
 a=25
|AC|=25√2
Ostrosłup jest "przechylony " w kierunku ściany SDC
O − rzut prostokątny punktu S na płaszczyznę
Tw. o trzech prostopadłych:
Prosta m jest prostopadła do prostej k, wtedy i tylko wtedy,
gdy jest prostopadła do prostej k'.
Narysowano wysokość h1, h1⊥BC − to jest oczywiste ,
OL jest rzutem prostokątnym h1 na płaszczyznę ABCD
Dalej mamy: KL⊥BC i KL⊥AD,
LO jest rzutem prostokątnym h1 na płaszczyznę ABCD
OK jest rzutem KS na płaszczyznę ABCD
⇔KS⊥KL
a=25
|AC|=25√2
Ostrosłup jest "przechylony " w kierunku ściany SDC
O − rzut prostokątny punktu S na płaszczyznę
Tw. o trzech prostopadłych:
Prosta m jest prostopadła do prostej k, wtedy i tylko wtedy,
gdy jest prostopadła do prostej k'.
Narysowano wysokość h1, h1⊥BC − to jest oczywiste ,
OL jest rzutem prostokątnym h1 na płaszczyznę ABCD
Dalej mamy: KL⊥BC i KL⊥AD,
LO jest rzutem prostokątnym h1 na płaszczyznę ABCD
OK jest rzutem KS na płaszczyznę ABCD
⇔KS⊥KL
 Jak powinny wyglądać moje
kroki w "konstruowaniu" takiego ostrosłupa? Czy tak?
1. Wyznaczam spodek wysokości ostrosłupa i szkicuję jego wysokość
2. Szkicuję wysokość h1, która pada obojętnie w jakim punkcie na ramię BC.
3. Rzut prostokątny h1 ma płaszczyznę podstawy
I teraz właśnie w mojej głowie pojawia się pytanie "W jakim dokładnie punkcie wysokość h2
powinna
upadać?". Tego nie potrafię jeszcze wykonać. Rozumiem, że jestem w stanie ten punkt padania h2
wyznaczyć posługując się twierdzeniem o trzech prostych prostopadłych?
Wiem Milu, że próbowałaś mi to wyjaśnić, ale na ten moment jeszcze nie umiem tego sposobu
myślenia przyswoić. Jeśli moje kroki są dobre to jutro spróbuję to przemyśleć jeszcze raz
Jak powinny wyglądać moje
kroki w "konstruowaniu" takiego ostrosłupa? Czy tak?
1. Wyznaczam spodek wysokości ostrosłupa i szkicuję jego wysokość
2. Szkicuję wysokość h1, która pada obojętnie w jakim punkcie na ramię BC.
3. Rzut prostokątny h1 ma płaszczyznę podstawy
I teraz właśnie w mojej głowie pojawia się pytanie "W jakim dokładnie punkcie wysokość h2
powinna
upadać?". Tego nie potrafię jeszcze wykonać. Rozumiem, że jestem w stanie ten punkt padania h2
wyznaczyć posługując się twierdzeniem o trzech prostych prostopadłych?
Wiem Milu, że próbowałaś mi to wyjaśnić, ale na ten moment jeszcze nie umiem tego sposobu
myślenia przyswoić. Jeśli moje kroki są dobre to jutro spróbuję to przemyśleć jeszcze raz 

 Dzień dobry
Dzień dobry  Zregenerowałem mózg i chyba na coś wpadłem. Oto jak rozumiem współliniowość punktów L, O i K
(przepraszam za oznaczenia małymi literami, ale nie wiem jak napisać wielkie).
1. Szkic ostrosłupa − nie jest to ostrosłup prawidłowy zatem jego spodek wysokości nie znajdzie
się
w punkcie przecięcia się przekątnych podstawy.
2. Szkicuję h1 i jej rzut prostokątny na płaszczyznę ABCD, dzięki temu otrzymuję punkt O.
3. W tym momencie mamy sytuację, w której mogę skorzystać z
twierdzenia o trzech prostych prostopadłych. Zatem na moim rysunku mamy: m ⊥ h1 ⇔ m ⊥ k.
4. Po drugiej stronie wysokości ostrosłupa mamy taką samą sytuację. Skoro ABCD to kwadrat
zatem znów pojawia się prosta m. Więc: m ⊥ h2 ⇔ m ⊥ k.
Z kroków 3 i 4 wynika, że punkty K, O, L są współliniowe. Czy tak to powinienem rozumieć?
Zregenerowałem mózg i chyba na coś wpadłem. Oto jak rozumiem współliniowość punktów L, O i K
(przepraszam za oznaczenia małymi literami, ale nie wiem jak napisać wielkie).
1. Szkic ostrosłupa − nie jest to ostrosłup prawidłowy zatem jego spodek wysokości nie znajdzie
się
w punkcie przecięcia się przekątnych podstawy.
2. Szkicuję h1 i jej rzut prostokątny na płaszczyznę ABCD, dzięki temu otrzymuję punkt O.
3. W tym momencie mamy sytuację, w której mogę skorzystać z
twierdzenia o trzech prostych prostopadłych. Zatem na moim rysunku mamy: m ⊥ h1 ⇔ m ⊥ k.
4. Po drugiej stronie wysokości ostrosłupa mamy taką samą sytuację. Skoro ABCD to kwadrat
zatem znów pojawia się prosta m. Więc: m ⊥ h2 ⇔ m ⊥ k.
Z kroków 3 i 4 wynika, że punkty K, O, L są współliniowe. Czy tak to powinienem rozumieć?
 Będę wiedział na przyszłość
Będę wiedział na przyszłość
 Najprościej tutaj to będzie, jeśli przetniesz ostrosłup płaszczyzną prostopadłą do
ABCD wyznaczoną przez punkty: S, O i taką, aby krawędź przecięcia była równoległa do AB.
Najprościej tutaj to będzie, jeśli przetniesz ostrosłup płaszczyzną prostopadłą do
ABCD wyznaczoną przez punkty: S, O i taką, aby krawędź przecięcia była równoległa do AB.


 Tak wynosi ona 25. Rozwiązałem już to zadanie dziś rano. Wrzucę to może ktoś skorzysta:
Punkty K, O, L są współliniowe co wynika z twierdzenia o trzech prostych prostopadłych:
|BC| ⊥ |OL| ⇔ |BC| ⊥ |SL| zatem |BC| ⊥ |OL| i |BC| ⊥ |SL|
Skoro |AD| || |BC| to taka sama sytuacja dzieje się na ścianie ADS.
P△BCS = P△ABS = 250
P△ADS = P△DCS = 187,5
Tak wynosi ona 25. Rozwiązałem już to zadanie dziś rano. Wrzucę to może ktoś skorzysta:
Punkty K, O, L są współliniowe co wynika z twierdzenia o trzech prostych prostopadłych:
|BC| ⊥ |OL| ⇔ |BC| ⊥ |SL| zatem |BC| ⊥ |OL| i |BC| ⊥ |SL|
Skoro |AD| || |BC| to taka sama sytuacja dzieje się na ścianie ADS.
P△BCS = P△ABS = 250
P△ADS = P△DCS = 187,5
