matura 2014 czerwiec inne rozwiązanie marek: Zadanie 10 odstawą ostrosłupa jest kwadrat ABCD o boku długości 25. Ściany boczne ABS i BCS mają takie same pola, każde równe 250. Ściany boczne ADS i CDS też mają jednakowe pola, każde równe 187,5. Krawędzie boczne AS i CS mają równe długości. Oblicz objętość tego ostrosłupa. Ma ktoś pomysł rozwiązać inaczej te zadanie niż podane na stronie https://matematykaszkolna.pl/strona/4127.html

Metis: A czego nie rozumiesz w tym rozwiązaniu ?

Bogdan:

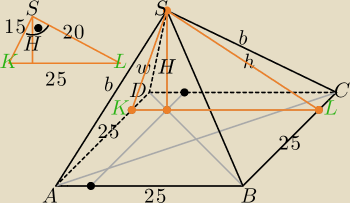
	25h
W trójkącie BCS:		= 250 ⇒ h = 20.
	2

	25w
W trójkącie ADS:		= 187,5 ⇒ w = 15.
	2

Widać, że 15² + 20² = 25², a więc trójkąt KLS jest prostokątny.

	1		1		15*20
Pole trójkąta KLS: P =		*15*20 i P =		*25*H, stąd wysokość H=		= 12.
	2		2		25

	1
Objętość ostrosłupa V =		*252*12 = 2500
	3

marek: @Metis Wszystko rozumiem,ale chciałbym poznać inny sposób,aby mieć większe pole manewru na maturze Bogdan dzięki

Monia : Że wzoru Herona też można policzyć pole i potem wysokość. Ja dokładnie wpadłam na rozwiązanie te co ty. Tylko jedno mnie zastanawia. Jak matematyczne udowodnić, że KD=LC. Ja mam inaczej to pokazane, inne oznaczenia, ale dokładnie tak samo jak Ty to rozwiązałam. Tylko brakuje mi dowodu że podstawą tego trójkąta jest faktycznie nasze a=25

??: Dokladnie, skad wiadomo, ze KL =25?

KLS:

	ab
c=
	h

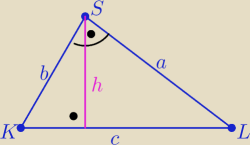
	15*20
|KL|=		= .......... = 25
	12

as: KD=LC bo KL||DC a to już z twierdzenia o trzech prostych prostopadłych(SL,OS,BC i KS,OK,AD), gdzie O to spodek wysokości ostrosłupa. przynajmniej moim zdaniem tak jest