Prawdopodobieństwo, 3 różne punkty - otrzymaj trójkąt.
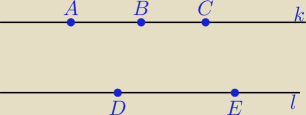
Muszyna: Dane są dwie proste równoległe k i l.
Na prostej k wybrano 3 różne punkty, a na prostej l dwa różne punkty.
Oblicz prawdopodobieństwo tego, że losując dowolne 3 punkty otrzymamy trójkąt o wierzchołkach w
tych punktach.
Dziękuje bardzo za odpowiedź, bądź jakieś naprowadzenie.
Pozdrawiam.

16 kwi 16:18
wredulus_pospolitus:
Rozumiem, że losujemy wierzchołki z TYCH 5 punktów.
Zastanów się KIEDY wybrane trzy punkty NIE UTWORZĄ trójkąta.
Tak więc −−− liczysz prawdopodobieństwo zdarzenia przeciwnego.
1 − obliczone .... i po krzyku
16 kwi 16:27
wredulus_pospolitus:
Jedna uwaga −−− 'kiedy trzy punkty NIE UTWORZĄ trójkąta' to de facto problem z geometrii −−−
pomyśl przez chwilę nad tym.
16 kwi 16:29
Mila:
16 kwi 18:14
Muszyna: Dziękuje ślicznie Mila oraz wredulus
pospolitus.
Miłego wieczoru dla państwa, pozdrawiam.

16 kwi 18:46
Miłościwy: Dlaczego w |A| = 9? Według twoich rachunków naliczyłem 6. i 5/3 to 10? Sądziłem, że są to
silnie, ale nie.
16 kwi 18:54
16 kwi 19:28
wredulus_pospolitus:
Miłościwy −−− wiesz co to jest dwumian Newtona

16 kwi 19:42
Mila:
Pewnie zna tylko regułę mnożenia?
16 kwi 21:05



