Wykładnicza i logarytmiczna smiemas2: Zastosuj własności logarytmów do obliczenia wartości wyrażeń a)log₁₁77−2log₁₁√7 b) 16^log₂3 Przedstaw liczbę w postaci a^x, a∊N⁺ a)√13√13√13 pierwszy pierwiastek jest na wszystkie, drugi do kolejnego, wiecie.

	22π+9π
b)
	36π−1

Zapisz wyrażenie log₃63−2 w postaci logarytmu o podstawie 2 Rozwiąż graficznie:

	34−x		√121
−2(x+1)2+3=		+(√3+2)0−
	81		11

błagam was, jeślit o napisze to będę miał dwójkę XD

Jerzy:

	77
a) = log1177 − log11(√7)2 = log1177 − log117 = log11(		)
	7

= log₁₁11 = 1

Maciess: No to musisz to na pisać, powodzenia! Jakies własne próby? Z ktorym konkretnie masz problem?

smiemas2: generalnie, mam czas do godziny 13:20, pani mnie zaskoczyła i bez przygotowań raczej średnio, żebym to napisał teraz sam

Maciess: b) Skorzystaj z a^log_ab=b

Jerzy: Nie opowiadaj,że zadała ci to przed chwilą.

smiemas2: :(

smiemas2: No poważnie, o 12:16

Maciess: W przykładzie z tymi pierwiastkami są tylko 3 liczby? Czy one 'lecą w nieskończoność'?

smiemas2: tylko trzy liczby, jeden duży pierwiastek, który zawiera wszystkie te pierwiastki z trzynastu

Jerzy:

	1
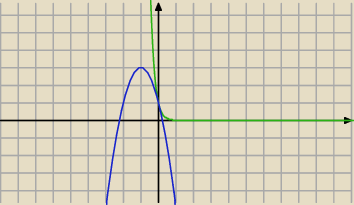
Graficznie: −2(x+1)2 +3 =
	81x

x = 0

a7: b) 16=2⁴ 2^4log₂3=2^log₂34=3⁴=81

Maciess: Z tymi pierwiastkami, rozbijając to na iloczyn pierwiastkow otrzymujemy 13^1/2*13^1/4*13^1/8=13^1/2+1/4+1/8=13^7/8

smiemas2: jeszcze tylko to! Zapisz wyrażenie log₃63−2 w postaci logarytmu o podstawie 2

Jerzy:

	log27
= log363 − log39 = log3(63/9) = log37 =
	log23

a7:

	63		log27
log363−2=log363−log39=log3		=log37=
	9		log23

smiemas2: kocham was, serio, przestudiuje to i obiecuje ze sam śmigne te zadanka nastepnym razem!

a7:

a7: https://matematykaszkolna.pl/strona/218.html