małe pytanko Chila: Tekst zadania: Podstawą ostrosłupa jest trójkąt o bokach 10, 10 i 16 długości .Krawędzie boczne tego ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 60 stopni. Oblicz objętość tego ostrosłupa. Jak połowa obwodu podstawy pomnożona razy promień może być równa polu podstawy?

wredulus_pospolitus: Razy oczywiście promień okręgu WPISANEGO w tą podstawę, tak Wynika to ze wzoru:

	2PΔ
r =
	a+b+c

https://matematykaszkolna.pl/strona/542.html Jak nadal masz wątpliwości to możesz wyprowadzić sobie tenże wzór na promień okręgu wpisanego w trójkąt.

wredulus_pospolitus: a bardzo łatwo (szybko) można wyprowadzić tenże wzór

wredulus_pospolitus: PS. a raczej powyższy wzór wynika z faktu o który pytasz (bo de facto udowodniasz to o co pytasz i później z tego można wyznaczyć wzór na promień, który napisałem)

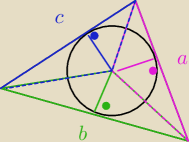
aniabb: Pole zielonego b*r/2 pole niebieskiego c*r/2 pole różowego a*r/2 razem to Pole całego trójkąta P = (a+b+c)*r/2

aniabb: tyle że w treści zadania jest kąt do krawędzi więc spodkiem wysokości jest środek okręgu opisanego

aniabb:

	abc
zatem bardziej pasuje wzór P=
	4R

aniabb:

	25√3
i H=R√3 =
	3

	400√3
zatem V=
	3

Chila: dzięks