kwadrat Graf: Kwadrat ABCD ma długość boku 2. Niech P będzie punktem środkowym AD. Odcinki AC i BP przecinają się w punkcie Q. Promień największego koła zawartego w QCDP można zapisać w postaci a−√b, gdzie a, b są liczbami naturalnymi oraz b jest liczbą bezkwadratowa. Oblicz wartość a + b. Liczba bezkwadratowa: https://pl.wikipedia.org/wiki/Liczba_bezkwadratowa

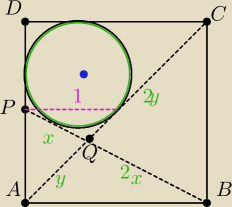
a7: |PB|=√5=3x x=√5/3

	4√2
AC=2√2=3y 2y=
	3

	2P		1   2*3   6		19
r=		=		=
	x+2y+1+2		√5/3+(4√2)/3+3		√5+4√2+9

i co dalej?

Graf: A czemu tak dzielimy na x i 2x orz y i 2y skąd to wynika?

a7: trójkąty APQ i BCQ są podobne więc boki CB=2PA,(PA jest to połówa boku Da czyli równe połowie CB gdyż jest kwadrat) więc reszta boków w tej samej skali tutaj teoria https://matematykaszkolna.pl/strona/531.html

a7: może ktoś wymyśli jeszcze rozwiązanie, bo to, co policzyłam to może być w ogóle zły trop...

Graf: Ale chyba z tego wyniku nie wyjdzie a−√b

a7: no właśnie chyba nie, dlatego to może być zły trop

Graf: Nie wiadomo czemu b ma być tą liczbą bezkwadratową.

Mila: To koło nie może być styczne do wszystkich boków tego czworokąta. Trzeba wybrać kąt w który będzie to koło wpisane.