Wyznaczenie wierzchołków kwadratu - geometria analityczna Shizzer: Punkt A=(1, −1) jest wierzchołkiem kwadratu opisanego na okręgu o równaniu x² + y² − 4y −1 = 0. Znajdź pozostałe wierzchołki tego kwadratu. Znalazłem link z rozwiązaniem tego zadania: https://matematykaszkolna.pl/forum/233854.html Ale niestety nie rozumiem wszystkich rzeczy zawartych w tym rozwiązaniu. Policzyłem punkt C z tego, że Równanie okręgu: x² + (y − 2)² = 5 S = (0, 2), r = √5 AS→ = SC→ AS→ = [0−1, 2+1] = [−1, 3] C = (−1, 5) Punkt B można policzyć w jakiś sposób z prostopadłości AS→ ⊥ BS→. Wiem, że wektory są prostopadłe wtedy kiedy ich iloczyn skalarny jest równy 0. Próbowałem ten fakt wykorzystać: AS→ * BS→ = 0 AS→ = [−1, 3] BS→ = [0 − x_b, 2 − y_b] = [−x_b, 2 − y_b] [−1 * −x_b, 3 * (2 − y{b})] = [x_b, 6 − 3y_b] = 0 Zapewne przydałoby się ułożyć jakiś układ równań, który pozwoliłby mi to równanie zapisać za pomocą jednej niewiadomej. Proszę o wytłumaczenie mi tego zadania, bo nie ukrywam, że w działaniach na wektorach dopiero zbieram potrzebne mi doświadczenie i miejscami się gubię. Być może po prostu jeszcze nie widzę wielu rzeczy, które mógłbym wykorzystać.

Shizzer: Źle napisałem. Nie rozumiem NIEKTÓRYCH rzeczy z podanego wyżej rozwiązania, a nie wszystkich

wredulus_pospolitus: to nie działaj na wektorach jeżeli masz z nimi problem. I metoda alternatywna: Krok 1) wyznaczasz prostą zawierającą AS Krok 2) wyznaczasz punkt C leżący na tej prostej (opis współrzędnych) taki, że środek odcinka AC jest punktem S Krok 3) wyznaczasz prostopadłą do (1) przechodzącą przez punkt S Krok 4) wyznaczasz punkty B i D na prostej (3) będące odległe od punktu S o wartość |AS|

wredulus_pospolitus: II metoda alternatywna: Krok 1) wyznaczasz |AS| Krok 2) zapisujesz równanie okręgu o środku w S i promieniu |AS| Krok 3) wyznaczasz prostą zawierającą A i S Krok 4) z układu równań (2) i (3) wyznaczysz współrzędne punktu A (który już masz) i punktu C Krok 5) wyznaczasz prostopadłą do (3) przechodzącą przez S Krok 6) z układu równań (3) i (5) wyznaczasz współrzędne punktu B i D

wredulus_pospolitus: W kroku 6 oczywiście powinno być: z układu równań (2) i (5) wyznaczasz współrzędne punktu B i D

Maciess: Ale tu chyba rachunek wektorowy bedzie najprostszy i najoszczędniejszy w zapisie.

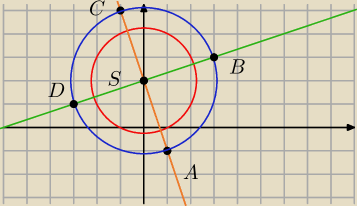
Saizou : bez wektorów 1) wszystkie wierzchołki kwadratu ABCD leżą na okręgu o równaniu s: x²+(y−2)²=10 (r=|SA|) 2) prosta SA ma równanie l: y=−3x+2 3) prosta prostopadła do l i przechodząca przez punkt S ma równanie

	1
k: y=		x+2
	3

4) punkty przecięcia się prostej k oraz okręgu s to szukane wierzchołki x²+(y−2)²=10

	1
y=		x+2
	3

Saizou : Spóźniłem się

wredulus_pospolitus: Maciess −−− jest najprostszy ... podaję alternatywę w momencie w którym ktoś ma problemy z wektorami

wredulus_pospolitus: Saizou −−− bo Ty 'za ładnie' próbujesz robić

Saizou : Chyba tak, ale rysunek to podstawa

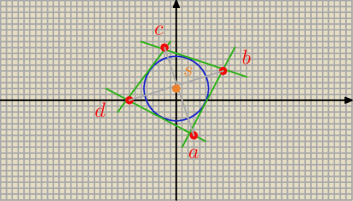
Shizzer: Rysunek może nie jest zbyt piękny, ale starałem się. Zostawię tutaj rozwiązanie zadania dla potomnych innym sposobem niż przy użyciu wektorów. Równanie okręgu: x² + (y − 2)² = 5 ⇒ S = (0, 2), r = √5 Wyznaczenie równania prostej |AS|:

⎧	2 = b
⎩	−1 = a + b

−1 = a + 2 a = −3 ⇒ y = −3x + 2 Punkt S jest środkiem okręgu oraz odcinka |AC|: S = (0, 2) = ((x_c + 1) / 2, (y_c − 1) / 2)

⎧	xc + 1 = 0
⎩	yc − 1 = 4

⎧	xc = −1
⎩	yc = 5	⇒ C = (−1, 5)

Równanie prostej |BD| prostopadłej do |AS|: −3a = −1 a = ¹₃

⎧	a = 13
⎩	b = 2

y = ¹₃x + 2 ⇒ 3y = x + 6 ⇒ x = 3y − 6 Punkty B i D leża na prostej |BD| zatem: B = (3b − 6, b), D = (3d − 6, d) gdzie b i d ∊ R |BS| = |DS| = |AS| |AS| = √1² + (−3)² = √10 Wyznaczenie współrzędnych punktu B: |BS| = √(3b − 6)² + (b − 2)² = √10 Liczby z obu stron są dodatnie zatem można podnieść obie strony równości do kwadratu. (3b − 6)² + (b − 2)² = 10 b = 1 ⋁ b = 3 B = (−3, 1) ⋁ B = (3, 3) Wyznaczenie współrzędnych punktu D: Powstaje taka sama równość jak powyżej, ale niewiadomą jest d, a nie b. Wystarczy wziąć teraz przeciwne współrzędne jako wynik. D = (−3, 1) ⋁ D = (3, 3) Zgodnie z rysunkiem powinno być tak: A = (1, −1), B = (3, 3), C = (−1, 5), D = (−3, 1). Pytają o współrzędne wszystkich punktów oprócz A, więc: (3, 3), (−1, 5), (−3, 1).

Shizzer: Długie te obliczenia wyszły. Mógłby ktoś mi pomóc zrozumieć lepiej wektory i rozwiązać to zadanie również za ich pomocą? Tylko bardzo byłoby mi miło gdyby zostały dodane jakieś opisy tłumaczące poszczególne kroki rozwiązania wtedy. Na maturze czas jest bardzo ważny dlatego działania na wektorach mogłyby mi się zapewne przydać.

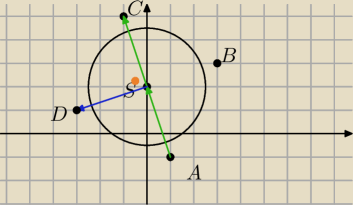
Saizou : Niech C=(x_c, y_c) AS^→=SC^→ (S dzieli przekątną AC na dwa równe odcinki) [0−1; 2−(−1)]=[x_c−0; y_c−2] −1=x_c. oraz 3=y_c−2→y_c=5 C=(−1, 5) ==== AS^→ jest prostopadły do SD^→ (przekątne kwadratu są prostopadłe) AS^→= [−1, 3] SD^→= [x_d; y_d−2] AS^→ o SD^→ = 0 (iloczyn skalarny jest równy zero) 0 =−x_d+3(y_d−2) x_d=3y_d−6 SD^→=[3y_d−6; y_d] |SD^→|=|AS^→| (przekątne dzielą się w połowie) − od razu podnosimy do kwadratu (3y_d−6)²+y_d²=3²+1² ... doliczasz y_d1 oraz y_d2, będą to współrzędne punktów D oraz B PS. sprawdź rachunki

Shizzer: Bardzo dziękuję! Wszystko rozumiem. Spróbuję porozwiązywać więcej tego typu zadań na wektorach