Punkt A=(1,−1) jest wierzchołkiem kwadratu opisanego na okręgu x2 + y2 − 4y − 1 Zosia: Punkt A=(1,−1) jest wierzchołkiem kwadratu opisanego na okręgu x2 + y2 − 4y − 1 = 0 Znajdź pozostałe wierzchołki tego kwadratu. Rozwiązuję układ równań, ale C= (−1, 5) AB→+BC→ = AC→

	|AC|
AB→⊥BC→ i |AB| = |BC| =
	√2

z tego układu wyjdą punkty B i D |AB| = √ (x_b − 1)² + (y_b + 1)² |BC|= √ (−1 − x_b)² + (5 − y_b)² |AC|= √10 − które równania porównać ze sobą? lub wektory AB→ =[x_b −1, y_b + 1] BC→=[−1 − x_c, y_c − 5 ] AC→= [−2, 4]

Zosia: ponawiam

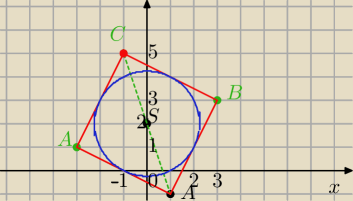
Mila: x² + y² − 4y − 1 = 0 ⇔ x²+(y−2)²−4−1=0 x²+(y−2)²=5 , r=√5, S=(0,2) Przekątne są prostopadłe, równe i dzielą się na połowy. SA^→[1,−3] SB^→⊥SA^→ SB^→=[3,1] S(0,2)→T_[3,1]→B(0+3,2+1)=(3,3) S(0,2)→T_[−3,−1]→A(0−3,2−1)=(−3,1)

Zosia: dziękuje