dowodowe bizi: W trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC. Wykaż, że prawdziwa jest równość |BC|²−|AC|²=|AB|*|AC| Hej wszystkim , rozwiązuję sobie mature próbną i dostałem takie zadanie chętnie wykorzystałbym tu twierdzenie cosinusów ,lecz nie wychodzi mi mógłby ktoś wykonać to zadanie wykorzystując tw.cosinusów? czekam na pomoc

wredulus_pospolitus: pokaż swoje rozumowanie skorzystać zapewne będziesz musiał i z jednego i z drugiego

ula: było https://matematykaszkolna.pl/forum/376361.html

wredulus_pospolitus: ula −−− jasne, że było ... przecież to powtórzony arkusz jest, jak zresztą reszta tej pożal się Boże matury próbnej.

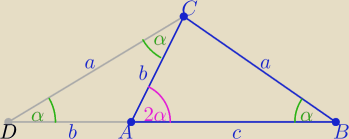
Eta: 1 sposób podałam tu 376361 Inny sposób też ( bez tw. cosinusów) ΔADC i DBC podobne i równoramienne zatem:

	a		b
		=		⇒ a2−b2=bc −−−− i mamy tezę
	b+c		a

|BC|²−|AC|²=|AB|*|AC| ====================

bizi: dzięki

Eta:

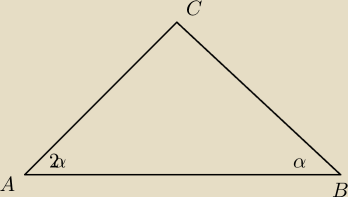
salamandra: A ja podam jeszcze inny:

|BC|		AC
	=
sin2α		sinα

BC*sinα=AC*sin2α BC*sinα=AC*2sinαcosα BC=AC*2cosα kąt ACB=180−3α

AB		AC
	=
sin3α		sinα

AB*sinα=AC*sin3α

	AC*sin3α		AC*sinα(3cos2α−sin2α)
AB=		=
	sinα		sinα

AB=AC*(3cos²α−sin²α) BC=AC*2cosα AB=AC*(3cos²α−sin²α) BC²−AC²=AC*(3cos²α−sin²α)*AC (AC²−4cos²α)−AC²=AC²*(3cos²α−sin²α) AC²(4cos²α−1)=AC²(3cos²α−sin²α) / : AC² 4cos²α−1=3cos²α−sin²α cos²α=1−sin²α cos²α=cos²α

Eta:

salamandra: