planimetria Alicja: W trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC. Wykaż, że prawdziwa jest równość |BC|² − |AC|² = |AB| ⋅| AC| .

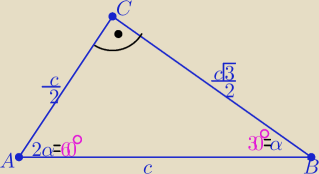
Eta: A może w treści jest ... "w trójkącie prostokątnym ABC..... wtedy 2α=60^o , α=30^o

	c√3		c
|BC|=		, |AC|=		, |AB|=c
	2		2

to

	3c2		c2		c2
L=|BC|2−|AC|2=		−		=
	4		4		2

	c		c2
P=|AB|*|AC|= c*		=
	2		2

L=P c.n.w

Alicja: nie, niestety w tresci nie jest powiedziane ze to trojkat prostokatny. To zadanie z tegorocznej czerwcowej matury rozszerzonej ...

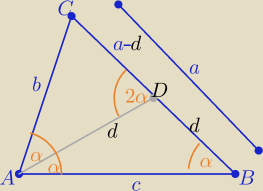Eta: Jeżeli trójkąt dowolny to tak: Oznaczam : |AB|=c, |AC|=b , |BC|=a d−− dwusieczna kąta BAC Z podobieństwa trójkątów ADC i ABC z cechy (kkk)

d		b		cb
	=		⇒ d=
c		a		a

i z tw. o dwusiecznej:

c		b		cb		a		ab
	=		i d=		⇒		=		⇒b2=a2−cb⇒
d		a−d		a		b		a2−cb

a²−b²=cb |BC|²−|AC|²=|AB|*|AC| ==================== c.n.w.

Alicja: bardzo dziekuje nie wpadlam na ten pomysl z dwusieczna ...